题目内容
(本小题满分12分)已知 均为正数,证明:
均为正数,证明: ,
,
并确定 为何值时,等号成立。
为何值时,等号成立。
 均为正数,证明:
均为正数,证明: ,
,并确定
 为何值时,等号成立。
为何值时,等号成立。见解析。
本试题主要是考查了运用不等式的思想来证明不等式问题的运用。
首先可以考虑运用分析法和综合法两种办法来完成,分别对于已知的关系式分析结构特点,然后结合均值不等式的思想也可以,也能通过重要不等式来证明。
(证法一)
∵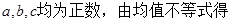
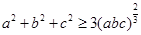 …………………………①
…………………………①
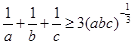 ,
,
∴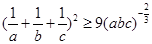 ……………………②
……………………②
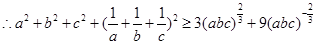
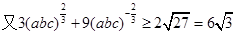 ……………………③
……………………③
∴原不等式成立。
当且仅当a=b=c时,①式和②式等号成立,当且仅当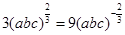 时,③式等号成立。
时,③式等号成立。
即当a=b=c=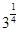 时原式等号成立。
时原式等号成立。
(证法二)∵a,b,c都是正数,由基本不等式得
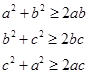
∴ ………………………………①
………………………………①
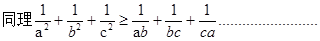 ②
②
∴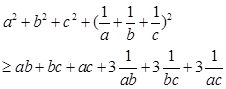
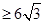 …………………………………………③
…………………………………………③
∴原不等式成立
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,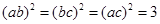 时,③式等号成立。
时,③式等号成立。
即当a=b=c=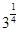 时原式等号成立。
时原式等号成立。
首先可以考虑运用分析法和综合法两种办法来完成,分别对于已知的关系式分析结构特点,然后结合均值不等式的思想也可以,也能通过重要不等式来证明。
(证法一)
∵
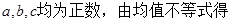
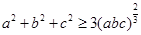 …………………………①
…………………………①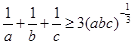 ,
,∴
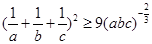 ……………………②
……………………②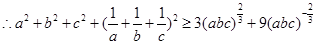
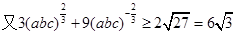 ……………………③
……………………③∴原不等式成立。
当且仅当a=b=c时,①式和②式等号成立,当且仅当
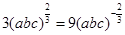 时,③式等号成立。
时,③式等号成立。即当a=b=c=
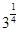 时原式等号成立。
时原式等号成立。(证法二)∵a,b,c都是正数,由基本不等式得
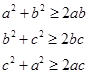
∴
 ………………………………①
………………………………①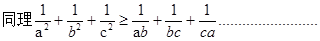 ②
②∴
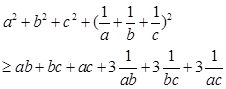
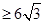 …………………………………………③
…………………………………………③∴原不等式成立
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,
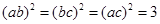 时,③式等号成立。
时,③式等号成立。即当a=b=c=
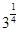 时原式等号成立。
时原式等号成立。
练习册系列答案
相关题目
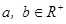 ,试证:
,试证: ;并求函数
;并求函数 (
( )的最小值.
)的最小值. ,证明:
,证明: .
.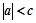
 ,求证:
,求证: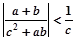 .
. ,对任意正数
,对任意正数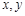 ,
, 始终可以是一个三角形的三条边,则实数m的取值范围为 .
始终可以是一个三角形的三条边,则实数m的取值范围为 . 
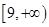
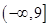
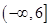
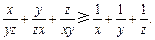
 、
、 、
、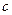 为实数,
为实数, ,则下列四个结论中正确的是( )
,则下列四个结论中正确的是( )


