题目内容
4.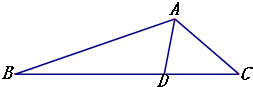 已知△ABC中,∠BAC=120°,AB=2,AC=1.AD是∠BAC的角平分线,交BC于D.
已知△ABC中,∠BAC=120°,AB=2,AC=1.AD是∠BAC的角平分线,交BC于D.(Ⅰ)求BD:DC的值;
(Ⅱ)求AD的长.
分析 (Ⅰ)在三角形ABD与三角形ACD中,分别利用正弦定理列出关系式,根据AD为角平分线,互补两角正弦值相等,即可求出BD:DC的值;
(Ⅱ)三角形ABC面积=三角形ABD面积+三角形ACD面积,利用三角形面积公式列出关系式,即可求出AD的长.
解答 解:(Ⅰ)在△ABD中,$\frac{AB}{sin∠ADB}$=$\frac{BD}{sin∠BAD}$,在△ACD中,$\frac{AC}{sin∠ADC}$=$\frac{CD}{sin∠CAD}$,
∵AD是∠BAC的角平分线,∠ADB+∠ADC=180°,
∴∠BAD=∠CAD,
∵sin∠ADB=sin∠ADC,且AB=2,AC=1,
则BD:DC=AB:AC=2:1;
(Ⅱ)∵∠BAC=120°,AD平分∠BAC,
∴∠BAD=∠CAD=60°,
∵S△ABC=S△ABD+S△ACD,即$\frac{1}{2}$AB•AC•sin∠BAC=$\frac{1}{2}$AB•AD•sin∠BAD+$\frac{1}{2}$AC•AD•sin∠CAD,
∴$\frac{1}{2}$×2×1×$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×AD×(2+1),
解得:AD=$\frac{2}{3}$.
点评 此题考查了正弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
16.在△ABC中,若a=4.b=3,c=2,则△ABC边BC的中线AD长为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{15}}{2}$ | D. | $\frac{5}{2}$ |
13.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:
算得,K2≈7.8.见附表:参照附表,得到的正确结论是( )
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别无关” |
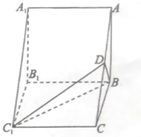 如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=BC,侧面A1B1BA和B1C1CB都是边长为2的正方形,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=BC,侧面A1B1BA和B1C1CB都是边长为2的正方形,D为AC的中点.