题目内容
若盒中装有同一型号的灯泡共10只,其中有8只合格品,2只次品
(1)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(2)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望
的分布列和数学期望
(1)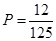 ;(2)X的分布列如下表:
;(2)X的分布列如下表:X 1 2 3 p 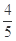
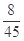
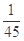
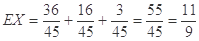
解析试题分析:(1)由于10只灯泡中有2只是次品,所以从中取一次恰好为次品的概率为: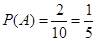
有放回连续取3次,则为3次独立重复试验,由独立重复试验概率公式得: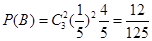
(2)由于盒只有2只灯泡是次品,所以最多取3次即可取得正品,由此知X的可能取值为1、2、3
X=1,表示第一次取到正品;X=2,表示第一次取到次品第二次取到正品;X=3表示第一次第二次取到次品第三次取到正品,由此即可得X的分布列进而求得X的期望
试题解析:(1)设一次取次品记为事件A,由古典概型概率公式得: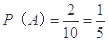 (2分)
(2分)
有放回连续取3次,其中2次取得次品记为事件B,由独立重复试验得: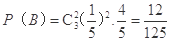 (5分)
(5分)
(2)依据知X的可能取值为1 2 3 (6分)
且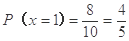 (7分)
(7分)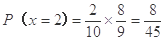 (8分)
(8分)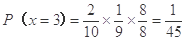 (9分)
(9分)
则X的分布列如下表:
(10分) X 1 2 3 p 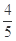
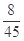
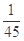
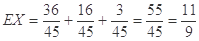 (12分)
(12分)
考点:1、古典概型;2、随机变量的分布列及期望

练习册系列答案
相关题目

 名学生被考官L面试,求
名学生被考官L面试,求
 个,从中任取
个,从中任取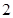 个都是白球的概率为
个都是白球的概率为 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取 个球,取出的球不放回,直到其中有一人取到白球时终止.用
个球,取出的球不放回,直到其中有一人取到白球时终止.用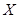 表示取球终止时取球的总次数.
表示取球终止时取球的总次数. .
. ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立. π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.