题目内容
甲、乙、丙三个车床加工的零件分别为350个,700个,1050个,现用分层抽样的方法随机抽取6个零件进行检验.
(1)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求其中至少有一个是乙车床加工的零件;
(2)从抽取的6个零件中任意取出3个,记其中是乙车床加工的件数为X,求X的分布列和期望.
(1) ;(2)分布列如图所示,
;(2)分布列如图所示, .
.
解析试题分析:本题主要考查分层抽样、条件概率、离散型随机变量的分布列和数学期望等基础知识,同时考查分析问题解决问题的的能力和计算求解能力.第一问,利用分层抽样中 ,列出表达式,解出每一层的零件个数,本问属于条件概率,
,列出表达式,解出每一层的零件个数,本问属于条件概率, ,先根据条件求
,先根据条件求 和
和 ,再求
,再求 ;第二问,本问属于离散型随机变量的分布列和数学期望问题,先写出随机变量X的可能取值,再利用超几何分布的概率公式计算出每种情况的概率,列出分布列,用
;第二问,本问属于离散型随机变量的分布列和数学期望问题,先写出随机变量X的可能取值,再利用超几何分布的概率公式计算出每种情况的概率,列出分布列,用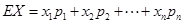 求数学期望.
求数学期望.
试题解析:(Ⅰ)由抽样方法可知,从甲、乙、丙三个车床抽取的零件数分别为1,2,3.
从抽取的6个零件中任意取出2个,记事件“已知这两个零件都不是甲车床加工点”为A,事件“其中至少有一个是乙车床加工的”为B,则 ,
, ,
,
所求概率为 . 5分
. 5分
(Ⅱ)X的可能取值为0,1,2. ,i=0,1,2.
,i=0,1,2.
X的分布列为
10分X 0 1 2 P 0.2 0.6 0.2
X的期望为 . 12分
. 12分
考点:1.分层抽样;2.条件概率;3.离散型随机变量的分布列和数学期望;4.超几何分布.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看作一个总体,从中任取一个分数
 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为 ,定义事件
,定义事件 {
{ ,且函数
,且函数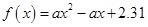 没有零点},求事件
没有零点},求事件 发生的概率.
发生的概率.  ,乙组能使生物成活的概率为
,乙组能使生物成活的概率为 ,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的. ,求
,求 ;
; ;
; ;
; 个等式并证明;
个等式并证明;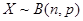 ,求证:
,求证: .
. 的分布列和数学期望
的分布列和数学期望