题目内容
若a,b,c均为实数,且a=x2-2y+![]() ,b=y2-2z+
,b=y2-2z+![]() ,c=z2-2x+
,c=z2-2x+![]() .求证:a,b,c中至少有一个大于0.
.求证:a,b,c中至少有一个大于0.
答案:
解析:
解析:
|
证明:(用反证法)假设a,b,c都不大于零,即a≤0,b≤0,c≤0则a+b+c≤0,而a+b+c=x2-2y+ 因为π>3,所以(x-1)2+(y-1)2+(z-1)2≥0,所以a+b+c>0. 这与a+b+c≤0矛盾,因此a,b,c中至少有一个大于0. |

练习册系列答案
相关题目
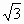 |a-kb|(k>0,k∈R).
|a-kb|(k>0,k∈R). (其中a>0,b>0).
(其中a>0,b>0).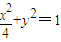 ,求a,b的值.
,求a,b的值. .
. ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;