Question

（本小题满分12分）已知直线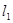的方程为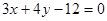，求满足下列条件的直线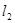的方程.

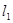（1）与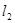平行且过点（-1，3）

（2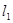）与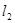垂直且与两坐标轴围成的三角形面积为4.

 

Answer 1

【答案】

（1）；(2) 或

【解析】(I)由于两条直线平行，可由l₁的斜率得到l₂的斜率，再根据直线l₂过点（-1，3），从而可写出点斜式方程再化成一般式即可.

（II）根据两直线垂直的条件可知两条直线的斜率互为负倒数，因而可求出l₂的斜率，设出直线l₂的方程，然后分别令x,y等于0,可得与坐标轴的交点坐标，从而根据与坐标轴围成的三角形的面积4,建立关于b的方程，求出b值，得到所求直线的方程.

解：（1）直线：，, 

 ∵∥  ∴，∴直线：  即

(2) ∵  ∴  设的方程为

则它与两坐标轴交点是    ∴

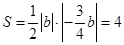
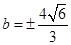∴  ∴直线的方程是或