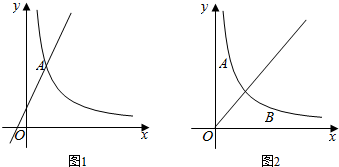题目内容
3.已知函数f(x)=x2+ax+3.(1)若f(x)≥a对x∈R恒成立,求实数a的取值范围;
(2)若f(x)≥a对x∈[-1,1]恒成立,求实数a的取值范围;
(3)若f(x)≥a对x∈[-2,1]恒成立,求实数a的取值范围.
分析 (1)利用△=a2-4(3-a)≤0,即可求实数a的取值范围;
(2)(3)将二次函数进行配方,利用二次函数的图象和性质求解,要使不等式f(x)≥0恒成立,则只需求出函数在区间上的最小值大于等于0即可.
解答 解:设函数h(x)=x2+ax+3-a,
(1)∵f(x)≥a对x∈R恒成立,
∴△=a2-4(3-a)≤0,
∴-2≤a≤6;
(2)在x∈[-1,1]时的最小值为g(a),
则①当对称轴x=-$\frac{a}{2}$<-1,即a>2时,g(a)=h(-1)=4-2a≥0,得a≤2,又a>2,此时不成立.
②当-$\frac{a}{2}$∈[-1,1]时,即-2≤a≤2时,g(a)=3-a-$\frac{{a}^{2}}{4}$≥0,得-6≤a≤2,故此时-2≤a≤2.
③当-$\frac{a}{2}$>1,即a<-2时,g(a)=h(1)=4≥0,成立,此时a<-2.
综上:a≤2.
(3)在x∈[-2,1]时的最小值为F(a),
则①当对称轴x=-$\frac{a}{2}$<-2,即a>4时,F(a)=h(-2)=7-3a≥0,得a≤$\frac{7}{3}$,又a>4,此时不成立.
②当-$\frac{a}{2}$∈[-2,1]时,即-2≤a≤4时,F(a)=3-a-$\frac{{a}^{2}}{4}$≥0,得-6≤a≤2,故此时-2≤a≤2.
③当-$\frac{a}{2}$>1,即a<-2时,F(a)=h(1)=4≥0,成立,此时a<-2.
综上:a≤2.
点评 本题主要考查二次函数的图象和性质,要注意分别讨论对称轴和区间之间的关系确定函数的最小值.

练习册系列答案
相关题目
 与
与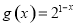 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )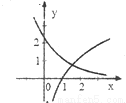 B.
B.
 D.
D.