题目内容
（本小题满分12分）
已知椭圆C：
＋
＝1（a＞b＞0）的左、右焦点为F1、F2，离心率为e. 直线
l：y＝ex＋a与x轴、y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，设
＝λ
.
（1）证明：λ＝1－e2；
（2）若
，△MF1F2的周长为6，求椭圆C的方程.
答案
.
所以点M的坐标是（
）. ………………4分
由
即
………………8分
证法二：因为A、B分别是直线l：
与x轴、y轴的交点，
所以A、B的坐标分别是
………………2分
设M的坐标是
所以
………………4分
因为点M在椭圆上，所以 
即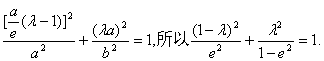
解得
………………8分
（2）当
时，
，所以
由△MF1F2的周长为6，得
……10分
所以
椭圆方程为
…………12分
练习册系列答案
百年学典课时学练测系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
