Question

（2013•绍兴一模）如图，在梯形ABCD中，AB∥CD，AB⊥AD，AD=4，点P在平面ABCD上的射影中点O，且PA=PD=2

3

，二面角P-AD-B为45°．
（1）求直线OA与平面PAB所成角的大小；
（2）若AB+BP=8求三棱锥P-ABD的体积．

Answer 1

分析：（1）过O点作OH⊥AB，垂足为H，连接PH．过O点作OK⊥PH，连接AK，证明∠OAK就是OA与平面PAB所成的角，求出OK、OA的长，即可求直线OA与平面PAB所成角的大小；
（2）利用AB+BP=8，求出AB的长，利用三棱锥P-ABD的体积V=

1

3

S△ABD•OP，即可求三棱锥P-ABD的体积．

解答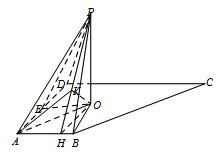：解：（1）过O点作OH⊥AB，垂足为H，连接PH．过O点作OK⊥PH，连接AK．
∵PO⊥平面ABCD，∴PO⊥AB．
∵OH⊥AB，∴AB⊥平面POH．
∵OK?平面POH，∴AB⊥OK，
∵OK⊥PH，∴OK⊥平面PAB．
∴∠OAK就是OA与平面PAB所成角．
∵PA=PD，
∴P点在平面ABCD上的射影O在线段AD的中垂线上，
设AD的中点为E，连接EP，EO，
∴EO⊥AD，EP⊥AD，∴∠PEO为二面角P-AD-B的平面角，∴∠PEO=45°．
在等腰△PAD中，∵AD=4，∴EA=ED=2，
∵PA=PD=2

3

．∴PE=2

2

．
在Rt△PEO中，OP=OE=2，∴OA=2

2

，
又∵OH=AE=2，PO=2，在Rt△POH中，可得OK=

2

∴sin∠OAK=

OK

OA

=

1

2

，∴∠OAK=30°，∴直线OA与平面PAB所成的角为30°．
（2）设AB=x，则PB=8-x，连接OB．
在Et△POB中，PB²=PO²+OB²，∵OE⊥AE，OE=AE，∴∠OAE=45°，∴∠OAB=45°．
在△OAB中，OB²=AO²+AB²-2AO•AB•cos∠OAB=8+x²-4x
∴4+8+x²-4x=（8-x）²，
∴x=

13

3

，即AB=

13

3

∴三棱锥P-ABD的体积V=

1

3

S△ABD•OP=

1

3

×

1

2

×4×

13

3

×2=

52

9

点评：本题考查线面角，考查三棱锥体积的计算，考查学生的计算能力，正确作出线面角是关键．