题目内容
已知f（x）的反函数f-1（x）=log2（x+2），则方程f（x-1）=0的根为（ ）
分析：由已知中f（x）的反函数f-1（x）=log2（x+2），我们可以求出函数f（x）的解析式，根据指数函数的单调性，可以将方程f（x-1）=0化为整式方程，解方程即可得到答案．
解答：解：∵f-1（x）=log2（x+2），
∴f（x）=2x-2
若f（x-1）=0
则2x-1-2=0
即x-1=1
解得x=2
故选D
∴f（x）=2x-2
若f（x-1）=0
则2x-1-2=0
即x-1=1
解得x=2
故选D
点评：本题考查的知识点是反函数，对数方程，其中根据已知中f（x）的反函数f-1（x）=log2（x+2），求出函数的解析式，是解答本题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
已知f（x）的反函数为f-1(x)=(
)x，则f（4-x2）的单调递减区间是（ ）
| 1 |
| 2 |
| A、（-2，0） |
| B、（-∞，0） |
| C、（0，+∞） |
| D、（0，2） |
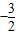
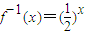，则f（4-x2）的单调递减区间是（ ）