题目内容
已知f（x）的反函数为f-1(x)=(
)x，则f（4-x2）的单调递减区间是（ ）
| 1 |
| 2 |
| A、（-2，0） |
| B、（-∞，0） |
| C、（0，+∞） |
| D、（0，2） |
分析：先依据求反函数的方法求出f（x）的解析式，再换元可得f（4-x2）的解析式，从而确定函数的单调减区间．
解答：解：∵f（x）的反函数为f-1(x)=(
)x，
∴f（x）=
，
f（4-x2）=
)，
在（-2，0）上函数值随自变量x的增大而减小，
故选 A．
| 1 |
| 2 |
∴f（x）=
| log | x
|
f（4-x2）=
| log | (4-x2
|
在（-2，0）上函数值随自变量x的增大而减小，
故选 A．
点评：本题考查求反函数的方法以及求函数的单调区间的方法，体现了换元的思想．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
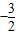
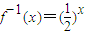，则f（4-x2）的单调递减区间是（ ）