题目内容
若圆锥的侧面展开图是半径为1cm、圆心角为180°的半圆,则这个圆锥的轴截面面积等于 .
【答案】分析:根据题意,该圆锥的底面半径r与满足关系式:2πr= ×2π×1,由此解出r=
×2π×1,由此解出r= .再由勾股定理算出高h之值,利用三角形面积公式即可得到该圆锥的轴截面面积.
.再由勾股定理算出高h之值,利用三角形面积公式即可得到该圆锥的轴截面面积.
解答:解:设该圆锥的底面半径为r,高为h,母线为l
∵圆锥的侧面展开图是半径为1cm、圆心角为180°的半圆,
∴母线l=1,且2πr= ×2π×1,解之得r=
×2π×1,解之得r=
∵r2+h2=l2,∴高h=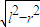 =
=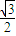
∵圆锥的轴截面是以底面直径为底,圆的高为高的等腰三角形
∴该圆锥的轴截面面积S= ×2r×h=
×2r×h=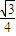
故答案为: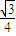
点评:本题给出圆锥的侧面展开图的形状和大小,求圆锥轴截面的面积,着重考查了圆锥的轴截面和圆锥的侧面展开图的认识等知识,属于基础题.
 ×2π×1,由此解出r=
×2π×1,由此解出r= .再由勾股定理算出高h之值,利用三角形面积公式即可得到该圆锥的轴截面面积.
.再由勾股定理算出高h之值,利用三角形面积公式即可得到该圆锥的轴截面面积.解答:解:设该圆锥的底面半径为r,高为h,母线为l
∵圆锥的侧面展开图是半径为1cm、圆心角为180°的半圆,
∴母线l=1,且2πr=
 ×2π×1,解之得r=
×2π×1,解之得r=
∵r2+h2=l2,∴高h=
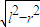 =
=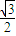
∵圆锥的轴截面是以底面直径为底,圆的高为高的等腰三角形
∴该圆锥的轴截面面积S=
 ×2r×h=
×2r×h=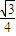
故答案为:
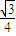
点评:本题给出圆锥的侧面展开图的形状和大小,求圆锥轴截面的面积,着重考查了圆锥的轴截面和圆锥的侧面展开图的认识等知识,属于基础题.

练习册系列答案
相关题目
 的扇形,则这个圆锥的表面积与侧面积的比是
的扇形,则这个圆锥的表面积与侧面积的比是