题目内容
(2012•房山区二模)已知定点M(1,2),点P和Q分别是在直线l:y=x-1和y轴上动点,则当△MPQ的周长最小值时,△MPQ的面积是( )
分析:作出M关于y轴的对称点M1,关于y=x-1的对称点M2,连接M1M2,与y轴交于Q点,与y=x-1交于P点,连接MQ,MP,此时△MPQ的周长最小,此时M1(-1,2),利用对称性求出M2坐标,确定出直线直线M1M2的解析式,进而确定出P与Q坐标,利用点到直线的距离公式求出M到直线M1M2的距离d,利用两点间的距离公式求出|PQ|的长,利用三角形面积公式求出即可.
解答: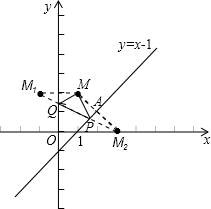 解:作出M关于y轴的对称点M1,关于y=x-1的对称点M2,连接M1M2,与y轴交于Q点,与y=x-1交于P点,连接MQ,MP,此时△MPQ的周长最小,
解:作出M关于y轴的对称点M1,关于y=x-1的对称点M2,连接M1M2,与y轴交于Q点,与y=x-1交于P点,连接MQ,MP,此时△MPQ的周长最小,
此时M1(-1,2),
∵直线MM2与y=x-1垂直,且y=x-1的斜率为1,
∴设直线MM2解析式为y=-x+b,
将M(1,2)代入得:2=-1+b,即b=3,
∴直线MM2解析式为y=-x+3,
与y=x-1联立得到A(2,1),
∴M2(3,0),
∴直线M1M2解析式为y-2=-
(x+1),即x+2y-3=0,
令x=0,得到y=
,即Q(0,
),
联立直线M1M2解析式与y=x-1求得P(
,
),
∵M到直线M1M2的距离d=
=
,|PQ|=
=
,
则S△MPQ=
|PQ|•d=
×
×
=
.
故选B
 解:作出M关于y轴的对称点M1,关于y=x-1的对称点M2,连接M1M2,与y轴交于Q点,与y=x-1交于P点,连接MQ,MP,此时△MPQ的周长最小,
解:作出M关于y轴的对称点M1,关于y=x-1的对称点M2,连接M1M2,与y轴交于Q点,与y=x-1交于P点,连接MQ,MP,此时△MPQ的周长最小,此时M1(-1,2),
∵直线MM2与y=x-1垂直,且y=x-1的斜率为1,
∴设直线MM2解析式为y=-x+b,
将M(1,2)代入得:2=-1+b,即b=3,
∴直线MM2解析式为y=-x+3,
与y=x-1联立得到A(2,1),
∴M2(3,0),
∴直线M1M2解析式为y-2=-
| 1 |
| 2 |
令x=0,得到y=
| 3 |
| 2 |
| 3 |
| 2 |
联立直线M1M2解析式与y=x-1求得P(
| 5 |
| 3 |
| 2 |
| 3 |
∵M到直线M1M2的距离d=
| 1+4-3 | ||
|
2
| ||
| 5 |
(0-
|
5
| ||
| 6 |
则S△MPQ=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 5 |
5
| ||
| 6 |
| 5 |
| 6 |
故选B
点评:此题考查了直线的一般式方程,点到直线的距离公式,两点间的距离公式,对称的性质,作出相应的图形,找出满足题意P与Q的位置是解本题的关键.

练习册系列答案
相关题目