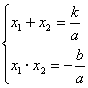题目内容
设抛物线y=ax2(a>0)与直线y=kx+b的两个交点的横坐标分别为x1,x2,而x3是直线与x轴的交点的横坐标,那么x1、x2、x3满足的关系是( )
A.x3=x1+x2
B.x3=![]()
C.x1x2=(x1+x2)·x3
D.x1x3=(x1+x3)·x2
答案:C
解析:
解析:
将y=kx+b代入抛物线方程y=ax2中 得ax2-kx-b=0,令其根为x1,x2 则有D=k2+4ab>0 而直线y=kx+b与x轴交点的横坐标x3=- 经验证,有x1·x2=(x1+x2)·x3 故选C |

练习册系列答案
相关题目