题目内容
[文]已知f（x）=ax，g（x）=logax（a＞0，且a≠1），若f（3）•g（3）＜0，那么f（x）与g（x）在同一坐标系内的图象可能是
- A.
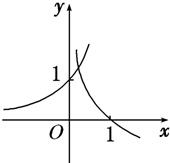
- B.
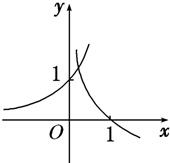
- C.
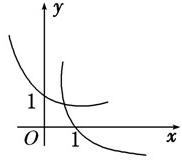
- D.
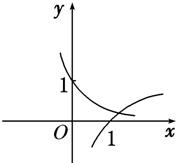
C
分析：由指数函数和对数函数的单调性知，f（x）=ax，g（x）=logax（a＞0，且a≠1）在（0，+∞）上单调性相同，
再由关系式f（3）•g（3）＜0即可选出答案．
解答：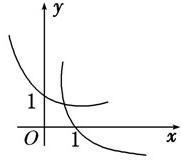
解：由指数函数和对数函数的单调性知，
f（x）=ax，g（x）=logax（a＞0，且a≠1），
在（0，+∞）上单调性相同，可排除A、D，
再由关系式f（3）•g（3）＜0可排除B
故选C．
点评：本题考查指数函数和对数函数的单调性，考查识图能力．
分析：由指数函数和对数函数的单调性知，f（x）=ax，g（x）=logax（a＞0，且a≠1）在（0，+∞）上单调性相同，
再由关系式f（3）•g（3）＜0即可选出答案．
解答：
解：由指数函数和对数函数的单调性知，f（x）=ax，g（x）=logax（a＞0，且a≠1），
在（0，+∞）上单调性相同，可排除A、D，
再由关系式f（3）•g（3）＜0可排除B
故选C．
点评：本题考查指数函数和对数函数的单调性，考查识图能力．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目