题目内容
(2013•怀化二模)对于定义域和值域均为[0,1]的函数f(x),定义f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn-1(x)),n=1,2,3,…满足fn(x)=x的点称为f的n阶周期点.设f(x)=
,则(1)方程f(x)=x的正根是
;(2)f的2阶周期点的个数是
|
| 2 |
| 3 |
| 2 |
| 3 |
4
4
.分析:本题考查的知识点是归纳推理,方法是根据已知条件和递推关系,先求出f的1阶周期点的个数,2阶周期点的个数,然后总结归纳其中的规律,f的n阶周期点的个数.
解答:解:(1)当0≤x≤
,方程f(x)=x 即 2x=x,解得 x=0,故方程没有正实数根.
当
<x≤1,方程f(x)=x 即 2-2x=x,解得x=
.
综上可得,方程f(x)=x的正根是
,
故答案为
.
(2)当x∈[0,
]时,f1(x)=2x=x,解得x=0;
当x∈(
,1]时,f1(x)=2-2x=x,解得x=
.
∴f的1阶周期点的个数是2.
当x∈[0,
]时,f1(x)=2x,方程f2(x)=x,即4x=x,解得x=0.
当x∈(
,
]时,f1(x)=2x,方程f2(x)=x,即2-4x=x,解得x=
.
当x∈(
,
]时,f1(x)=2-2x,方程f2(x)=x,即-2+4x=x,解得x=
.
当x∈(
,1]时,f1(x)=2-2x,方程f2(x)=x,即4-4x=x,解得x=
.
∴f的2阶周期点的个数是22=4,
故答案为 4.
| 1 |
| 2 |
当
| 1 |
| 2 |
| 2 |
| 3 |
综上可得,方程f(x)=x的正根是
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
(2)当x∈[0,
| 1 |
| 2 |
当x∈(
| 1 |
| 2 |
| 2 |
| 3 |
∴f的1阶周期点的个数是2.
当x∈[0,
| 1 |
| 4 |
当x∈(
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 5 |
当x∈(
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
当x∈(
| 3 |
| 4 |
| 4 |
| 5 |
∴f的2阶周期点的个数是22=4,
故答案为 4.
点评:本题主要考查函数的零点与方程的根的关系,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
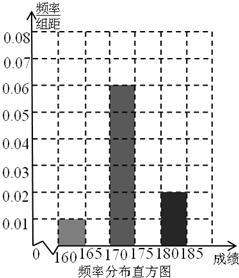 (2013•怀化二模)某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示.
(2013•怀化二模)某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示.