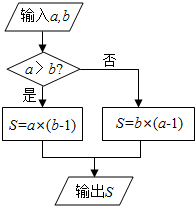
题目内容
18.已知f(x)=-x2+ax-a+6,x∈[0,1].(1)求f(x)的最小值g(a);
(2)若g(a)>a2,求a的取值范围.
分析 (1)先求出函数的对称轴,通过讨论a的范围,得到函数的单调性,从而求出函数的最小值,得到g(a)的解析式即可;
(2)分别解出关于不同范围内的a的不等式,取并集即可.
解答 解:(1)函数f(x)的对称轴是x=$\frac{a}{2}$,
当$\frac{a}{2}$≤0即a≤0时:f(x)在[0,1]递减,
g(a)=f(x)min=f(1)=5,
0<$\frac{a}{2}$<$\frac{1}{2}$即0<a<1时:f(x)在[0,$\frac{a}{2}$)递增,在($\frac{a}{2}$,1]递减,
g(a)=)=f(x)min=f(1)=5,
$\frac{1}{2}$≤$\frac{a}{2}$<1即1≤a<2时:f(x)在[0,$\frac{a}{2}$)递增,在($\frac{a}{2}$,1]递减,
g(a)=)=f(x)min=f(0)=6-a,
$\frac{a}{2}$≥1即a≥1时:f(x)在[0,1]递增,
g(a)=)=f(x)min=f(0)=6-a,
综上:g(a)=$\left\{\begin{array}{l}{5,a<1}\\{6-a,a≥1}\end{array}\right.$;
(2)由(1)得:a<1时:5>a2,解得:-$\sqrt{5}$<a<1,
a≥1时:6-a>a2,解得:1≤a<2,
故a的范围是:(-$\sqrt{5}$,2).
点评 本题考查了二次函数的性质,考查解不等式问题,考查分类讨论,是一道中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
9.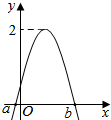 如图是函数$f(x)=Asin(2x+ϕ),(A>0,|ϕ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{2}$,则( )
如图是函数$f(x)=Asin(2x+ϕ),(A>0,|ϕ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{2}$,则( )
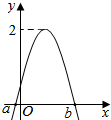 如图是函数$f(x)=Asin(2x+ϕ),(A>0,|ϕ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{2}$,则( )
如图是函数$f(x)=Asin(2x+ϕ),(A>0,|ϕ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{2}$,则( )| A. | f(x)在$(-\frac{3π}{8},\frac{π}{8})$上是增函数 | B. | f(x)在$(-\frac{3π}{8},\frac{π}{8})$上是减函数 | ||
| C. | f(x)在$(-\frac{5π}{12},\frac{π}{12})$上是增函数 | D. | f(x)在$(-\frac{5π}{12},\frac{π}{12})$上是减函数 |
10.函数f(x)=ax2+bx-2是定义在[1+a,2]上的偶函数,则f(x)在区间[-1,2]上的值域是( )
| A. | [-10,2] | B. | [-14,-2] | C. | (-∞,-2] | D. | [-14,-5] |