题目内容
如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直,且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°.(Ⅰ)求证:AC上平面BB1C1C;
(Ⅱ)求AB1与平面BB1C1C所成角的正切值;
(Ⅲ)在平面AA1B1B内找一点P,使三棱锥P-BB1C为正三棱锥,并求点P到平面BB1C的距离.

解:(1)∵面BB1C1C⊥面ABC,交线为BC,
AC⊥BC,∴AC⊥面BB1C1C
(Ⅱ)连B1C,由(1)知AC⊥平面BB1C1C,

∴∠CB1A就是AB1与平面BB1C1C所成的角.
取BB1中点E,连CE、AE,
在△CBB1中,BB1=BC=2,∠B1BC=60°,
∴△CBB1是正三角形,∴CE⊥BB1,
又AC⊥平面BB1C1C,.∴AE⊥BB1,
∴∠CEA为二面角A-BB1-C的平面角,∠CEA=30°
在Rt△CEA中,AC=CEtan30°=1,
∴在Rt△AB1C中,tan∠AB1C=![]() ,
,
(Ⅲ)在CE上取点P1,使![]() =2,
=2,
则P1为△B1BC的重心即中心.作P1P∥AC交AE于P
∵AC⊥平面BB1C1C,∴PP1⊥面BB1C1C,
即P在平面B1C1C上的射影是△BCB1中心
∴P- BB1C为正三棱锥,且![]() ,∴PP1=
,∴PP1=![]() ,
,
即P到平面BB1C的距离为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
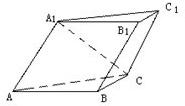 已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2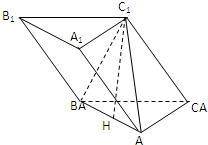 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.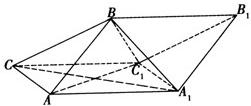 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点. (2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.
(2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.