题目内容
 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.(1)求证EF∥平面A1ACC1;
(2)求EF与侧面A1ABB1所成的角.
分析:(1)由题意可得:E是A1B中点.连A1C,所以EF∥A1C.再根据线面平行的判定定理可得线面平行.
(2)作FG⊥AB交AB于G,连EG,可得FG⊥平面A1ABB1,即可得到∠FEG是EF与平面A1ABB1所成的角,再在△EFG中利用解三角形的有关知识解决问题即可.
(2)作FG⊥AB交AB于G,连EG,可得FG⊥平面A1ABB1,即可得到∠FEG是EF与平面A1ABB1所成的角,再在△EFG中利用解三角形的有关知识解决问题即可.
解答: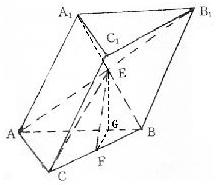 解:(1)证明:∵A1ABB1是菱形,E是AB1中点,
解:(1)证明:∵A1ABB1是菱形,E是AB1中点,
∴E是A1B中点.
连A1C,
∵F是BC中点,
∴EF∥A1C.
∵A1C?平面A1ACC1,EF?平面A1ACC1,
∴EF∥平面A1ACC1…(4分)
(2)作FG⊥AB交AB于G,连EG,
∵侧面A1ABB1⊥平面ABC且交线是AB,
∴FG⊥平面A1ABB1,
∴∠FEG是EF与平面A1ABB1所成的角
由AB=a,AC⊥BC,∠ABC=45°,得FG=
FB=
=BG
由AA1=AB=a,∠A1AB=60°,得EG=
a
∴tan∠FEG=
,
∴∠FEG=30°
所以EF与侧面A1ABB1所成的角为30°.
 解:(1)证明:∵A1ABB1是菱形,E是AB1中点,
解:(1)证明:∵A1ABB1是菱形,E是AB1中点,∴E是A1B中点.
连A1C,
∵F是BC中点,
∴EF∥A1C.
∵A1C?平面A1ACC1,EF?平面A1ACC1,
∴EF∥平面A1ACC1…(4分)
(2)作FG⊥AB交AB于G,连EG,
∵侧面A1ABB1⊥平面ABC且交线是AB,
∴FG⊥平面A1ABB1,
∴∠FEG是EF与平面A1ABB1所成的角
由AB=a,AC⊥BC,∠ABC=45°,得FG=
| ||
| 2 |
| a |
| 4 |
由AA1=AB=a,∠A1AB=60°,得EG=
| ||
| 4 |
∴tan∠FEG=
| ||
| 3 |
∴∠FEG=30°
所以EF与侧面A1ABB1所成的角为30°.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,以便熟悉几何体中的线面关系,再利用有关的定理与定义求出线面角.

练习册系列答案
相关题目
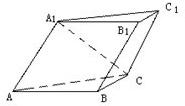 已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2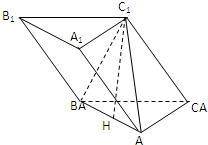 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.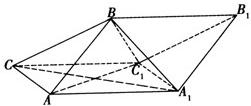 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为 (2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.
(2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.