题目内容
二项式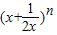 展开式中,前三项系数依次成等差数列,则展开式各项系数的和是( )
展开式中,前三项系数依次成等差数列,则展开式各项系数的和是( )A.28
B.27
C.
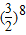
D.
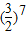
【答案】分析:求出数列的前3项的系数,利用前三项系数依次成等差数列,求出n,然后利用赋值法求出展开式各项系数的和.
解答:解:二项式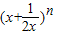 展开式中,前三项系数依次为
展开式中,前三项系数依次为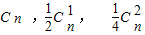 ;
;
因为前三项系数依次成等差数列,
所以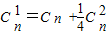 ,
,
即:n2-9n+8=0,解得n=8或n=1(舍去),
当x=1时二项式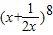 展开式各项系数的和是:
展开式各项系数的和是: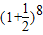 =
=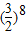 .
.
故选C.
点评:本题是基础题,考查等差数列的基本知识,二项式定理系数的性质,考查赋值法的应用,计算能力.
解答:解:二项式
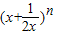 展开式中,前三项系数依次为
展开式中,前三项系数依次为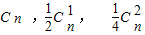 ;
;因为前三项系数依次成等差数列,
所以
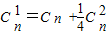 ,
,即:n2-9n+8=0,解得n=8或n=1(舍去),
当x=1时二项式
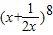 展开式各项系数的和是:
展开式各项系数的和是: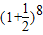 =
=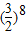 .
.故选C.
点评:本题是基础题,考查等差数列的基本知识,二项式定理系数的性质,考查赋值法的应用,计算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 展开式中的前三项系数成等差数列,则n的值为 .
展开式中的前三项系数成等差数列,则n的值为 .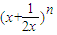 展开式中的前三项系数成等差数列,则n的值为 .
展开式中的前三项系数成等差数列,则n的值为 .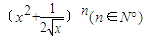 展开式中,前三项的二项式系数和是56,则展开式中的常数项为( )
展开式中,前三项的二项式系数和是56,则展开式中的常数项为( )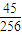
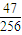
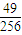
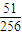
 展开式中的前三项系数成等差数列,则展开式中的常数项是 .
展开式中的前三项系数成等差数列,则展开式中的常数项是 . 展开式中的前三项系数成等差数列,则展开式中的常数项是 .
展开式中的前三项系数成等差数列,则展开式中的常数项是 .