题目内容
已知函数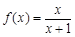 , 若数列
, 若数列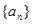 (n∈N*)满足:
(n∈N*)满足: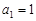 ,
,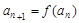
(1) 证明数列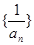 为等差数列,并求数列
为等差数列,并求数列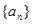 的通项公式;
的通项公式;
(2) 设数列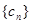 满足:
满足: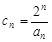 ,求数列
,求数列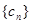 的前n项的和
的前n项的和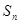 .
.
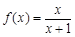 , 若数列
, 若数列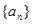 (n∈N*)满足:
(n∈N*)满足: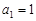 ,
,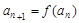
(1) 证明数列
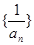 为等差数列,并求数列
为等差数列,并求数列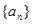 的通项公式;
的通项公式;(2) 设数列
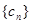 满足:
满足: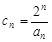 ,求数列
,求数列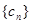 的前n项的和
的前n项的和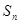 .
.(1) 证明见解析,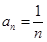 (2)
(2) 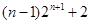
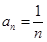 (2)
(2) 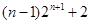
本试题主要是考查了数列通项公式的求解和数列求和的综合运用
(1)因为函数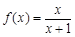 , 若数列
, 若数列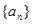 (n∈N*)满足:
(n∈N*)满足: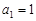 ,
,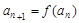 ,即
,即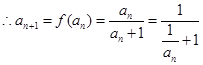
可知得到数列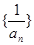 为等差数列,并得到数列
为等差数列,并得到数列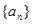 的通项公式;
的通项公式;
(2)设数列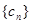 满足:
满足: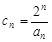 ,求数列
,求数列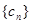 的前n项的和
的前n项的和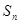 ,则利用错位相减法得到结论。
,则利用错位相减法得到结论。
解:(1)
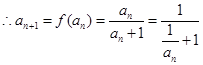

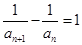
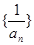 是等差数列,
是等差数列, 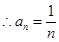 ……5分
……5分
(2)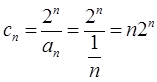
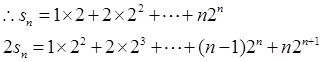
 ……10分
……10分
(1)因为函数
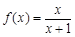 , 若数列
, 若数列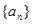 (n∈N*)满足:
(n∈N*)满足: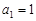 ,
,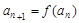 ,即
,即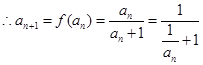
可知得到数列
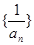 为等差数列,并得到数列
为等差数列,并得到数列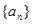 的通项公式;
的通项公式;(2)设数列
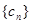 满足:
满足: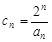 ,求数列
,求数列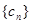 的前n项的和
的前n项的和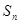 ,则利用错位相减法得到结论。
,则利用错位相减法得到结论。解:(1)

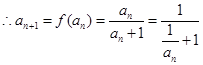

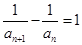
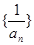 是等差数列,
是等差数列, 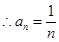 ……5分
……5分(2)
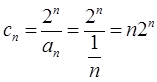
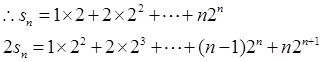
 ……10分
……10分
练习册系列答案
相关题目
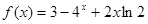 ,数列{an}满足:
,数列{an}满足: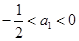 ,
,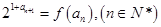 .
.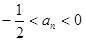
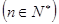 ;
;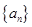 中,
中,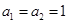 ,且
,且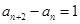 ,则数列
,则数列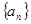 为等差数列,
为等差数列,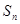 是等差数列的前
是等差数列的前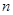 项和,已知
项和,已知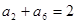 ,
,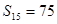 .
.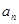 ;
;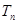 为数列
为数列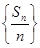 的前
的前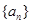 中,
中,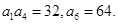
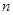 项和为
项和为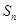 ,求
,求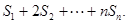
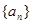 的前
的前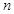 项和为
项和为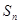 ,如果存在正整数
,如果存在正整数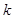 和
和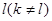 ,使得
,使得 ,
, ,则( )
,则( )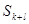 的最小值为
的最小值为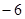
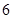
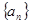 中
中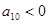 ,
, ,且
,且 ,则在
,则在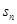 <0中,n的最大值为( )
<0中,n的最大值为( )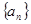 中,已知
中,已知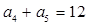 ,那么它的前8项和
,那么它的前8项和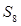 等于_________
等于_________