题目内容
设方程x2-px-q=0的解集为A,方程x2+qx-p=0的解集为B,若A∩B={1},则p= ,q= .
【答案】分析:若A∩B={1},则1是两个方程的根,再根据一元二次方程根的定义,所以p、q的值可求.
解答:解:∵A∩B={1},
∴一元二次方程方程x2-px-q=0,方程x2+qx-p=0的都有一个根是1,
根据一元二次方程根的定义,得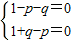
∴解得p=1,q=0
故答案为:1,0.
点评:本题考查了集合关系中的参数取值问题、一元二次方程的根的定义,属于基础题.
解答:解:∵A∩B={1},
∴一元二次方程方程x2-px-q=0,方程x2+qx-p=0的都有一个根是1,
根据一元二次方程根的定义,得
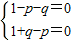
∴解得p=1,q=0
故答案为:1,0.
点评:本题考查了集合关系中的参数取值问题、一元二次方程的根的定义,属于基础题.

练习册系列答案
相关题目
设方程x2-px-q=0的解集为A,方程x2+qx-p=0的解集为B,若A∩B={1},则p+q=( )
| A、2 | B、0 | C、1 | D、-1 |