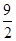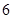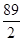题目内容
定义函数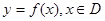 ,若存在常数
,若存在常数 ,对任意
,对任意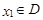 ,存在唯一
,存在唯一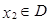 的,使得
的,使得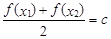 ,则称函数
,则称函数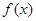 在
在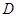 上的均值为
上的均值为 ,已知
,已知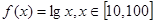 ,则函数
,则函数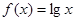 在
在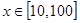 上的均值为( )
上的均值为( )
A. | B.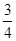 | C.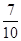 | D.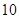 |
A
解析试题分析:根据定义,函数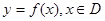 ,若存在常数
,若存在常数 ,对任意的
,对任意的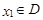 ,存在唯一的
,存在唯一的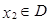 ,使得
,使得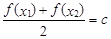 ,则称函数
,则称函数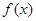 在
在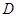 上的均值为
上的均值为 ,令
,令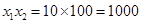 ,当
,当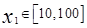 时,选定
时,选定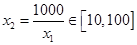 可得:
可得: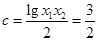 ,故选A.
,故选A.
考点:平均值不等式.

练习册系列答案
相关题目
设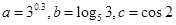 ,则( )
,则( )
A.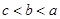 | B. | C.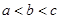 | D.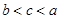 |
若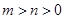 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.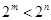 | B.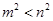 |
C.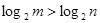 | D. |
幂函数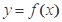 的图象经过点
的图象经过点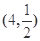 ,则
,则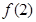 ( )
( )
A.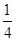 | B.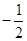 | C.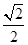 | D.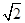 |
设函数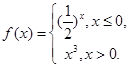 若
若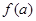 >1,则a的取值范围是
>1,则a的取值范围是
| A.(-1,1) | B.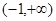 |
C.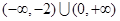 | D.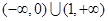 |
已知函数 对
对 的图象恒在x轴上方,则m的取值范围是( )
的图象恒在x轴上方,则m的取值范围是( )
A.2-2 <m<2+2 <m<2+2 | B.m<2 |
C.m<2+2 | D.m≥2+2 |
函数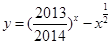 的零点的个数为( )
的零点的个数为( )
A. | B. | C. | D. |
设 ,则使函数
,则使函数 的值域为
的值域为 且为奇函数的所
且为奇函数的所 值为( )
值为( )
A. , , | B. , , | C. , , | D. , , , , |
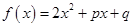 ,
,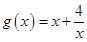 是定义在集合
是定义在集合 上的两个函数.对任意的
上的两个函数.对任意的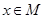 ,存在常数
,存在常数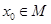 ,使得
,使得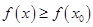 ,
,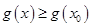 ,且
,且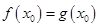 .则函数
.则函数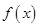 在集合
在集合 上的最大值为( )
上的最大值为( )