题目内容
将数列{an}中的所有项按每一行比上一行多两项的规则排成如下数表:
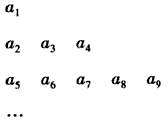
已知表中的第一列数a1,a2,a5…构成一个等差数列,记为{bn},且b2=4,b5=10。表中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn,
(1)求数列{bn}的通项公式;
(2)若上表中,从第二行起,每一行中的数按从左到右的顺序均构成等比数列,公比为同一个正数,且a13=1,
①求Sn;
②记M={n|(n+1)cn≥λ,n∈N*},若集合M的元素个数为3,求实数λ的取值范围。
(1)求数列{bn}的通项公式;
(2)若上表中,从第二行起,每一行中的数按从左到右的顺序均构成等比数列,公比为同一个正数,且a13=1,
①求Sn;
②记M={n|(n+1)cn≥λ,n∈N*},若集合M的元素个数为3,求实数λ的取值范围。
解:(1)设数列{bn}的公差为d,则 ,解得
,解得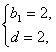 ,
,
所以bn=2n。
(2)①设每一行组成的等比数列的公比为q,
由于前n行共有1+3+5+…+(2n-1)=n2个数,且32<13<42,
所以a10=b4=8,所以a13=a10q3=8q3,
又a13=1,解得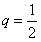 ,
,
因此 ,
,
所以,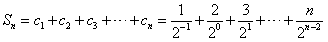 ,
,
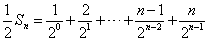 ,
,
因此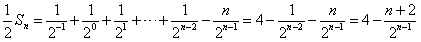 ,
,
解得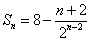 ;
;
②由①知,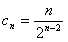 ,
,
不等式(n+1)cn≥λ,可化为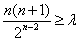 ,
,
设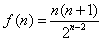 ,
,
计算得f(1)=4,f(2)=f(3)=6,f(4)=5,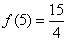 ,
,
因为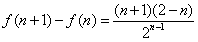 ,
,
所以当n≥3时,f(n+1)<f(n),
因为集合M元素的个数为3,
所以λ的取值范围是(4,5]。
 ,解得
,解得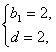 ,
,所以bn=2n。
(2)①设每一行组成的等比数列的公比为q,
由于前n行共有1+3+5+…+(2n-1)=n2个数,且32<13<42,
所以a10=b4=8,所以a13=a10q3=8q3,
又a13=1,解得
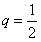 ,
,因此
 ,
,所以,
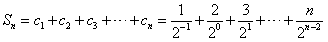 ,
,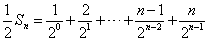 ,
,因此
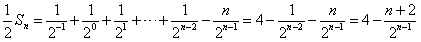 ,
,解得
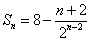 ;
;②由①知,
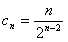 ,
,不等式(n+1)cn≥λ,可化为
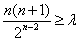 ,
,设
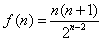 ,
,计算得f(1)=4,f(2)=f(3)=6,f(4)=5,
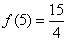 ,
,因为
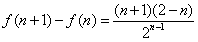 ,
,所以当n≥3时,f(n+1)<f(n),
因为集合M元素的个数为3,
所以λ的取值范围是(4,5]。

练习册系列答案
相关题目
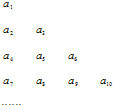 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表.记表中第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足2bn=bnSn-Sn2(n≥2,n∈N*).
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表.记表中第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足2bn=bnSn-Sn2(n≥2,n∈N*). 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表: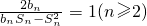 .
.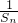 成等差数列,并求数列{bn}的通项公式;
成等差数列,并求数列{bn}的通项公式;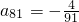 时,公比q的值.
时,公比q的值.
 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.