题目内容
下列结论:
①函数y=tan
在区间(-π,π)上是增函数;
②当x∈(1,+∞)时,函数y=x
,y=x2的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0;
④若函数f(x)=-丨x丨,若f(-m2-1)<f(2),则实数m∈(-∞,-1)∪(1,+∞);
其中所有正确结论的序号为
①函数y=tan
| x |
| 2 |
②当x∈(1,+∞)时,函数y=x
| 1 |
| 2 |
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0;
④若函数f(x)=-丨x丨,若f(-m2-1)<f(2),则实数m∈(-∞,-1)∪(1,+∞);
其中所有正确结论的序号为
①③④
①③④
.分析:①利用y=tanx在区间(-
,
)上是增函数即可判断①的正误;
②在同一坐标系中作出y=x
,y=x2与y=x的图象,即可判断其正误;
③利用函数的周期性即可判断;
④利用函数的奇偶性与单调性,通过解不等式m2+1>2即可作出判断.
| π |
| 2 |
| π |
| 2 |
②在同一坐标系中作出y=x
| 1 |
| 2 |
③利用函数的周期性即可判断;
④利用函数的奇偶性与单调性,通过解不等式m2+1>2即可作出判断.
解答: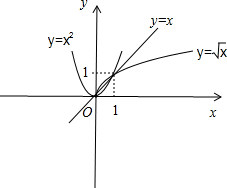 解:①∵y=tanx在区间(-
解:①∵y=tanx在区间(-
,
)上是增函数,
由-
<
<
得:x∈(-π,π),
∴函数y=tan
在区间(-π,π)上是增函数,①正确;
②作出函数y=x
,y=x2与y=x的图象,可知②错误;
③∵f(x)为R上的奇函数,
∴f(0)-0;
f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),即f(x)是以4为周期的函数,
∴f(6)=f(4+2)=f(2)=f(0)=0,故③正确;
④∵函数f(-x)=-丨-x丨=-|x|=f(x),
∴f(x)=-|x|为偶函数,
又f(x)=-|x|在(0,+∞)上单调递减,
∴由f(-m2-1)<f(2)得:m2+1>2,
解得m>1或m<-1.
故④正确.
综上所述,所有正确结论的序号为①③④.
故答案为:①③④.
 解:①∵y=tanx在区间(-
解:①∵y=tanx在区间(-| π |
| 2 |
| π |
| 2 |
由-
| π |
| 2 |
| x |
| 2 |
| π |
| 2 |
∴函数y=tan
| x |
| 2 |
②作出函数y=x
| 1 |
| 2 |
③∵f(x)为R上的奇函数,
∴f(0)-0;
f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),即f(x)是以4为周期的函数,
∴f(6)=f(4+2)=f(2)=f(0)=0,故③正确;
④∵函数f(-x)=-丨-x丨=-|x|=f(x),
∴f(x)=-|x|为偶函数,
又f(x)=-|x|在(0,+∞)上单调递减,
∴由f(-m2-1)<f(2)得:m2+1>2,
解得m>1或m<-1.
故④正确.
综上所述,所有正确结论的序号为①③④.
故答案为:①③④.
点评:本题 考查函数单调性、奇偶性、周期性,考查分析推理能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目