题目内容
我们把由半椭圆 (x≥0)与半椭圆
(x≥0)与半椭圆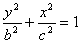 (x≤0)合成的曲线称作“果圆”,其中a2=
(x≤0)合成的曲线称作“果圆”,其中a2=
b2+c2,a>0,b>c>0。
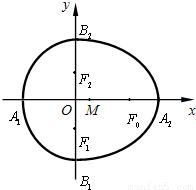
如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点,
(1)若△F0F1F2是边长为1的等边三角形,求该 “果圆”的方程;
(2)设P是“果圆”的半椭圆 (x≤0)上任意一点,求证:当|PM|取得最小值时,P在点
(x≤0)上任意一点,求证:当|PM|取得最小值时,P在点
B1,B2或A1处;
(3)若P是“果圆”上任意一点,求|PM|取得最小值时点P的横坐标。
 (x≥0)与半椭圆
(x≥0)与半椭圆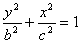 (x≤0)合成的曲线称作“果圆”,其中a2=
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0。
如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点,
(1)若△F0F1F2是边长为1的等边三角形,求该 “果圆”的方程;
(2)设P是“果圆”的半椭圆
 (x≤0)上任意一点,求证:当|PM|取得最小值时,P在点
(x≤0)上任意一点,求证:当|PM|取得最小值时,P在点B1,B2或A1处;
(3)若P是“果圆”上任意一点,求|PM|取得最小值时点P的横坐标。

解:(1)∵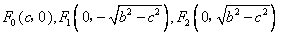 ,
,
∴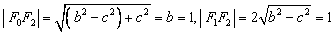 ,
,
于是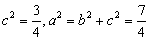 ,
,
所求“果圆”方程为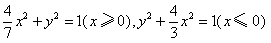 。
。
(2)设P(x,y),则
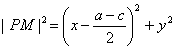
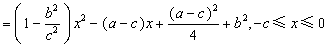 ,
,
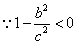 ,
,
∴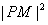 的最小值只能在x=0或x=-c处取到,
的最小值只能在x=0或x=-c处取到,
即当|PM|取得最小值时,P在点B1,B2或A1处;
(3) ,且B1和B2同时位于“果圆”的半椭圆
,且B1和B2同时位于“果圆”的半椭圆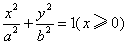 和半椭圆
和半椭圆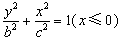 上,
上,
所以,由(2)知,只需研究P位于“果圆”的半椭圆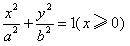 上的情形即可,
上的情形即可,

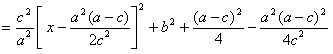 ,
,
当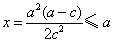 ,即a≤2c时,
,即a≤2c时,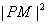 的最小值在
的最小值在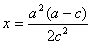 时取到,
时取到,
此时P的横坐标是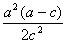 ;
;
当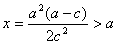 ,即a>2c时,由于
,即a>2c时,由于 在x<a时是递减的,
在x<a时是递减的,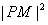 的最小值在x=a时取到,
的最小值在x=a时取到,
此时P的横坐标是a;
综上所述,若a≤2c,当|PM|取得最小值时,点P的横坐标是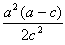 ;
;
若a>2c,当|PM|取得最小值时,点P的横坐标是a或-c。
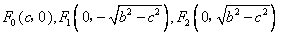 ,
, ∴
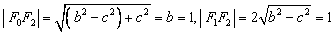 ,
,于是
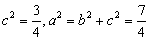 ,
,所求“果圆”方程为
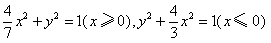 。
。(2)设P(x,y),则
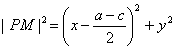
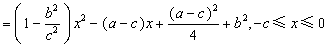 ,
,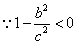 ,
,∴
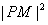 的最小值只能在x=0或x=-c处取到,
的最小值只能在x=0或x=-c处取到,即当|PM|取得最小值时,P在点B1,B2或A1处;
(3)
 ,且B1和B2同时位于“果圆”的半椭圆
,且B1和B2同时位于“果圆”的半椭圆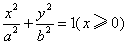 和半椭圆
和半椭圆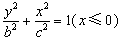 上,
上,所以,由(2)知,只需研究P位于“果圆”的半椭圆
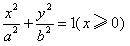 上的情形即可,
上的情形即可,
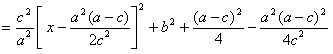 ,
,当
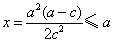 ,即a≤2c时,
,即a≤2c时,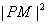 的最小值在
的最小值在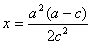 时取到,
时取到,此时P的横坐标是
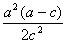 ;
;当
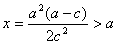 ,即a>2c时,由于
,即a>2c时,由于 在x<a时是递减的,
在x<a时是递减的,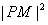 的最小值在x=a时取到,
的最小值在x=a时取到,此时P的横坐标是a;
综上所述,若a≤2c,当|PM|取得最小值时,点P的横坐标是
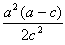 ;
;若a>2c,当|PM|取得最小值时,点P的横坐标是a或-c。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
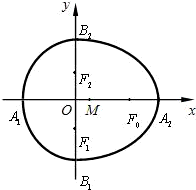 我们把由半椭圆
我们把由半椭圆 (x≥0)与半椭圆
(x≥0)与半椭圆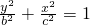 (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
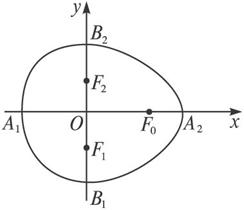
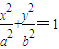 (x≥0)与半椭圆
(x≥0)与半椭圆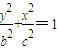 (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.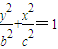 (x≤0)上任意一点.求证:当|PM|取得最小值时,P在点B1,B2或A1处;
(x≤0)上任意一点.求证:当|PM|取得最小值时,P在点B1,B2或A1处;