题目内容

图6
我们把由半椭圆![]() =1(x≥0)与半椭圆
=1(x≥0)与半椭圆![]() =1(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.
=1(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.
如图6,点F0、F1、F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x、y轴的交点.〔(文)M是线段A1A2的中点〕
(1)(理)若△F0F1F2是边长为1的等边三角形,求“果圆”的方程.
(2)(理)当|A1A2|>|B1B2|时,求![]() 的取值范围.
的取值范围.
(文)设P是“果圆”的半椭圆![]() =1(x≤0)上任意一点,求证:当|PM|取得最小值时,P在点B1、B2或A1处.
=1(x≤0)上任意一点,求证:当|PM|取得最小值时,P在点B1、B2或A1处.
(3)(理)连结“果圆”上任意两点的线段称为“果圆”的弦.试研究:是否存在实数k,使斜率为k的“果圆”平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的k值;若不存在,请说明理由.
(文)若P是“果圆”上任意一点,求|PM|取得最小值时点P的横坐标.
解:(1)(理)∵F0(c,0),F1(0,![]() ),F2(0,
),F2(0,![]() ),
),
∴|F0F2|=![]() =b=1,|F1F2|=
=b=1,|F1F2|=![]() =1.
=1.
于是c2=![]() ,a2=b2+c2=
,a2=b2+c2=![]() ,所求“果圆”方程为
,所求“果圆”方程为![]() x2+y2=1(x≥0),y2+
x2+y2=1(x≥0),y2+![]() x2=1(x≤0).
x2=1(x≤0).
(2)(理)由题意,得a+c>2b,即![]() >2b-a.
>2b-a.
∵(2b)2>b2+c2=a2,∴a2-b2>(2b-a)2,得![]() <
<![]() .
.
又b2>c2=a2-b2,∴![]() >
>![]() .∴
.∴![]() ∈(
∈(![]() ,
,![]() ).
).
(文)设P(x,y),则|PM|2=(x![]() )2+y2=(1
)2+y2=(1![]() )x2-(a-c)x+
)x2-(a-c)x+![]() +b2,-c≤x≤0,∵1
+b2,-c≤x≤0,∵1![]() <0,
<0,
∴|PM|2的最小值只能在x=0或x=-c处取到,即当|PM|取得最小值时,P在点B1、B2或A1处.
(3)(理)设“果圆”C的方程为![]() =1(x≥0),
=1(x≥0),![]() =1(x≤0).
=1(x≤0).
记平行弦的斜率为k.
当k=0时,直线y=t(-b≤t≤b)与半椭圆![]() =1(x≥0)的交点是P(a
=1(x≥0)的交点是P(a![]() ,t),与半椭圆
,t),与半椭圆![]() =1(x≤0)的交点是Q(-c
=1(x≤0)的交点是Q(-c![]() ,t).
,t).
∴P、Q的中点M(x,y)满足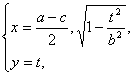 得
得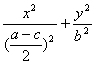 =1.
=1.
∵a<2b,∴![]() ≠0.
≠0.
综上所述,当k=0时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
当k>0时,以k为斜率过B1的直线l与半椭圆![]() =1(x≥0)的交点是(
=1(x≥0)的交点是(![]() ).
).
由此,在直线l右侧,以k为斜率的平行弦的中点轨迹在直线y=![]() x上,即不在某一椭圆上.
x上,即不在某一椭圆上.
当k<0时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
(文)∵|A1M|=|MA2|,且B1和B2同时位于“果圆”的半椭圆![]() =1(x≥0)和半椭圆
=1(x≥0)和半椭圆![]() =1(x≤0)上,∴由(2)知,只需研究P位于“果圆”的半椭圆
=1(x≤0)上,∴由(2)知,只需研究P位于“果圆”的半椭圆![]() =1(x≥0)上的情形即可.
=1(x≥0)上的情形即可.
|PM|2=(x![]() )2+y2=
)2+y2=![]() [x
[x![]() ]2+b2+
]2+b2+![]() .
.
当x=![]() ≤a,即a≤2c时,|PM|2的最小值在x=
≤a,即a≤2c时,|PM|2的最小值在x=![]() 时取到,此时P的横坐标是
时取到,此时P的横坐标是![]() .
.
当x=![]() >a,即a>2c时,由于|PM|2在x<a时是递减的,|PM|2的最小值在x=a时取到,此时P的横坐标是a.
>a,即a>2c时,由于|PM|2在x<a时是递减的,|PM|2的最小值在x=a时取到,此时P的横坐标是a.
综上所述,若a≤2c,当|PM|取得最小值时,点P的横坐标是![]() ;若a>2c,当|PM|取得最小值时,点P的横坐标是a或-c.
;若a>2c,当|PM|取得最小值时,点P的横坐标是a或-c.
