题目内容
【题目】已知m，n∈R＋，f(x)＝|x＋m|＋|2x－n|.
(1)当m＝n＝1时，求f(x)的最小值；
(2)若f(x)的最小值为2，求证
.
【答案】(1) 
. (2)见解析.
【解析】试题分析：（1）代入m＝n＝1，却掉绝对值，得到分段函数，判定分段函数的单调性，确定函数的最小值；
（2）由题意得，函数的最小值为2，得
，利用基本不等式求解最值，即可证明.
试题解析：
(1)∵f(x)＝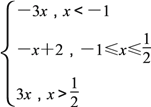
∴f(x)在(－∞，
)是减函数，在(，＋∞)是增函数，∴当x＝时，f(x)取最小值
.
(2)∵f(x)＝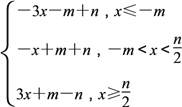
，
∴f(x)在(－∞，
)是减函数，在(，＋∞)是增函数，
∴当x＝时，f(x)取最小值f()＝m＋.
∵m，n∈R，∴
＋
＝ (＋)(m＋)
＝
(2＋
＋
)≥2
点晴:本题主要考查了绝含有绝对值的函数的最小值问题及分段函数的图象与性质、基本不等式的应用，属于中档试题，着重考查了分类讨论思想与转化与化归思想的应用，本题的解答中，根据绝对值的概念合理去掉绝对值号，转化为分段函数，利用分段函数的图象与性质，确定函数的最小值，构造基本不等式的条件，利用基本不等式是解答问题的关键.
练习册系列答案
相关题目
