题目内容
17.已知球O与棱长均为4$\sqrt{2}$的四面体ABCD的各条棱都相切,则平面ABC截球的截面面积为$\frac{8}{3}$π.分析 将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线,根据球O与正四面体的各棱都相切,可得球O的直径为正方体的棱长,从而可求平面ABC截球的截面面积.
解答 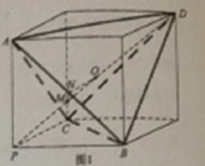 解:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线.
解:将正四面体ABCD,补成正方体,则正四面体ABCD的棱为正方体的面上对角线.
∵正四面体ABCD的棱长为4$\sqrt{2}$
∴正方体的棱长为4
∵球O与正四面体的各棱都相切,
∴球O的直径为正方体的棱长4,
设平面ABC截球O的截面圆的圆心为M,圆M与AB相切于点N,则OM⊥平面ABC,如图2所示,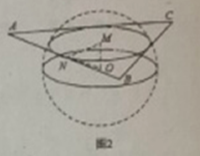
由正方体性质知M为体对角线PD与平面ABC的交点,且OM=$\frac{1}{6}$PD=$\frac{1}{6}$×$4\sqrt{3}$=$\frac{2\sqrt{3}}{3}$,
在Rt△OMN中,MN=$\sqrt{O{N}^{2}-O{M}^{2}}$=$\sqrt{\frac{8}{3}}$,
∴平面ABC截球的截面面积为$\frac{8}{3}$π.
故答案为:$\frac{8}{3}$π.
点评 本题考查球的表面积公式解题的关键是将正四面体ABCD,补成正方体,属于中档题..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.设a,b∈R+,且a≠b,则有( )
| A. | $\frac{a+b}{2}$<$\sqrt{ab}$<$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ | B. | $\sqrt{ab}$<$\frac{a+b}{2}$<$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ | ||
| C. | $\sqrt{ab}$<$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$<$\frac{a+b}{2}$ | D. | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$<$\sqrt{ab}$<$\frac{a+b}{2}$ |
2.从3名男同学和4名女同学中选2人分别担任学生会主席和副主席,则不同的选法种数为( )
| A. | 7 | B. | 21 | C. | 42 | D. | 12 |
6.(文)已知复数z=6+8i,则-|z|=( )
| A. | -5 | B. | -10 | C. | $\frac{14}{9}$ | D. | -$\frac{16}{9}$ |
7.已知复数z=2-i,则$\frac{z+1}{\overline{z}-1}$的虚部为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |