题目内容
已知函数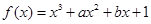 的导数
的导数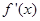 满足
满足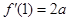 ,
,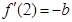 ,其中常数
,其中常数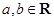 ,求曲线
,求曲线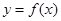 在点
在点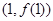 处的切线方程.
处的切线方程.
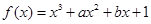 的导数
的导数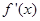 满足
满足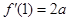 ,
,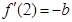 ,其中常数
,其中常数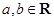 ,求曲线
,求曲线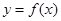 在点
在点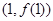 处的切线方程.
处的切线方程.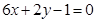
本试题主要考查了导数在研究函数中的运用。首先求解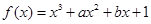 的解析式,由已知
的解析式,由已知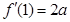 ,所以
,所以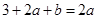 . 解得
. 解得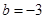 和由已知
和由已知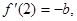 所以
所以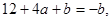 解得
解得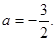 得到,然后
得到,然后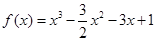 ,又因为
,又因为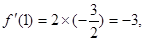
故曲线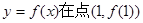 处的切线方程为
处的切线方程为
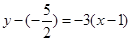 ,解得。
,解得。
解:因为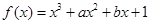 ,所以
,所以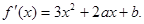
令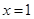 得
得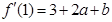 .
.
由已知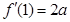 ,所以
,所以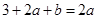 . 解得
. 解得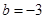 .
.
又令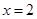 得
得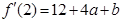 .
.
由已知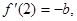 所以
所以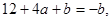 解得
解得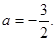
所以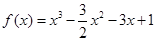 ,
,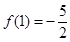 .
.
又因为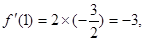
故曲线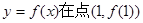 处的切线方程为
处的切线方程为
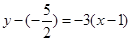 ,即
,即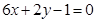 .
.
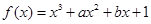 的解析式,由已知
的解析式,由已知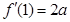 ,所以
,所以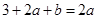 . 解得
. 解得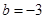 和由已知
和由已知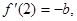 所以
所以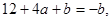 解得
解得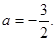 得到,然后
得到,然后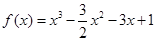 ,又因为
,又因为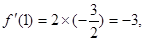
故曲线
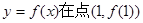 处的切线方程为
处的切线方程为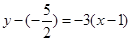 ,解得。
,解得。解:因为
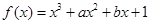 ,所以
,所以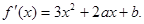
令
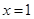 得
得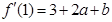 .
. 由已知
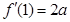 ,所以
,所以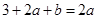 . 解得
. 解得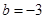 .
. 又令
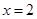 得
得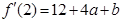 .
. 由已知
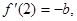 所以
所以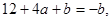 解得
解得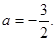
所以
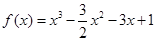 ,
,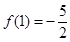 .
. 又因为
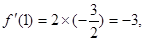
故曲线
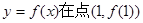 处的切线方程为
处的切线方程为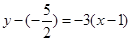 ,即
,即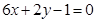 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
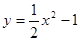 在点
在点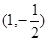 处切线的倾斜角为( )
处切线的倾斜角为( )


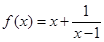 ,曲线
,曲线 过点
过点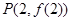 处的切线与直线
处的切线与直线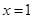 和直线
和直线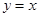 所围三角形的面积为_________。
所围三角形的面积为_________。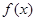 的导数为
的导数为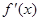 ,下列说法正确的有________.
,下列说法正确的有________.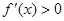 的解集为函数的增区间.
的解集为函数的增区间.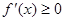 .
.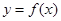 有
有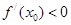 ,则该曲线在
,则该曲线在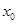 点处的切线的倾斜角一定( )
点处的切线的倾斜角一定( )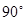 ;
;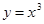 上过点(2,8)的切线方程为
上过点(2,8)的切线方程为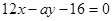 ,则实数
,则实数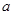 的值为( )
的值为( )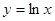 在点
在点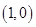 处的切线方程为________.
处的切线方程为________. 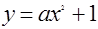 ,该曲线
,该曲线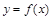 以点
以点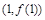 处的切线平行于直线
处的切线平行于直线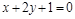 ,则该曲线的切线方程 .
,则该曲线的切线方程 .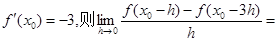 ___________.
___________.