题目内容
已知a为实数,函数f(x)=(x2+1)(x+a).(1)若f'(-1)=0,求函数y=f(x)在[-
 ,1]上的最大值和最小值;
,1]上的最大值和最小值;(2)若函数f(x)的图象上有与x轴平行的切线,求a的取值范围.
【答案】分析:(1)利用f'(-1)=0,可求得函数解析式,进而可研究函数的单调性,从而确定极值,进而可知最值;
(2)根据切线与横轴平行,对函数求导,使得到函数等于0有实根,得到关于一元二次方程的判别式,求出结果.
解答:解:(1)∵f'(-1)=0,∴3-2a+1=0,即a=2. …(2分)
∴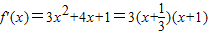 .
.
由f'(x)>0,得x<-1或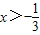 ; …(4分)
; …(4分)
由f'(x)<0,得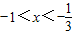 .因此,函数f(x)的单调增区间为
.因此,函数f(x)的单调增区间为 ,
,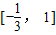 ;
;
单调减区间为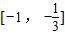 . …(6分)
. …(6分)
f(x)在x=-1取得极大值为f(-1)=2;f(x)在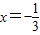 取得极小值为
取得极小值为 .
.
由∵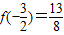 ,f(1)=6且
,f(1)=6且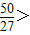
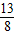
∴f(x)在[- ,1]上的最大值为f(1)=6,最小值为
,1]上的最大值为f(1)=6,最小值为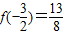 . …(8分)
. …(8分)
(2)∵f(x)=x3+ax2+x+a,∴f'(x)=3x2+2ax+1.
∵函数f(x)的图象上有与x轴平行的切线,∴f'(x)=0有实数解. …(10分)
∴△=4a2-4×3×1≥0,∴a2≥3,即 .
.
因此,所求实数a的取值范围是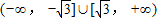 . …(12分)
. …(12分)
点评:本题考查函数的极值点应用,考查利用导数求函数的最值,考查学生分析解决问题的能力.
(2)根据切线与横轴平行,对函数求导,使得到函数等于0有实根,得到关于一元二次方程的判别式,求出结果.
解答:解:(1)∵f'(-1)=0,∴3-2a+1=0,即a=2. …(2分)
∴
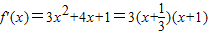 .
.由f'(x)>0,得x<-1或
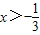 ; …(4分)
; …(4分)由f'(x)<0,得
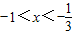 .因此,函数f(x)的单调增区间为
.因此,函数f(x)的单调增区间为 ,
,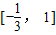 ;
;单调减区间为
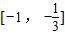 . …(6分)
. …(6分)f(x)在x=-1取得极大值为f(-1)=2;f(x)在
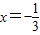 取得极小值为
取得极小值为 .
.由∵
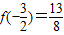 ,f(1)=6且
,f(1)=6且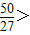
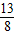
∴f(x)在[-
 ,1]上的最大值为f(1)=6,最小值为
,1]上的最大值为f(1)=6,最小值为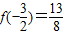 . …(8分)
. …(8分)(2)∵f(x)=x3+ax2+x+a,∴f'(x)=3x2+2ax+1.
∵函数f(x)的图象上有与x轴平行的切线,∴f'(x)=0有实数解. …(10分)
∴△=4a2-4×3×1≥0,∴a2≥3,即
 .
.因此,所求实数a的取值范围是
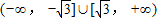 . …(12分)
. …(12分)点评:本题考查函数的极值点应用,考查利用导数求函数的最值,考查学生分析解决问题的能力.

练习册系列答案
相关题目