题目内容
7.已知对于任意实数x,均有f(π-x)=-f(x)与f(2π-x)=f(x)成立,当x∈[0,$\frac{π}{2}$]时,有f(x)=x2,试求f($\frac{59π}{11}$)的值.分析 结合三角函数的性质,得到f(x)是以2π为周期的周期函数,从而求出函数值.
解答 解:∵f(π-x)=-f(x),f(2π-x)=f(x),
∴f(π-x)=-f(2π-x),
用x+π换x:
得:f(-x)=-f(π-x),
故f(-x)=f(2π-x),
∴f(x)是以2π为周期的周期函数
∴f($\frac{59π}{11}$)=f(6π-$\frac{7π}{11}$)=f(π-$\frac{4π}{11}$)=-f($\frac{4π}{11}$)=-${(\frac{4π}{11})}^{2}$=-$\frac{1{6π}^{2}}{121}$.
点评 本题考查了三角函数问题,考查了函数的周期性,是一道基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2.焦点在x轴上的椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的离心率是$\frac{1}{2}$,则实数m的值是( )
| A. | 4 | B. | $\frac{9}{4}$ | C. | 1 | D. | $\frac{3}{4}$ |
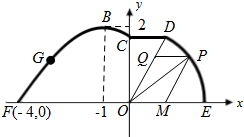 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,