题目内容
3.已知t为常数,且0<t<1,函数g(x)=$\frac{1}{2}$(x+$\frac{1-t}{x}$)(x>0)最小值和函数h(x)=$\sqrt{{x}^{2}-2x+2+t}$的最小值都是函数f(x)=-x3+ax2+bx(a,b∈R)的零点.(1)用含a的式子表示b,并求出a的取值范围;
(2)求函数f(x)在区间[1,2]上的最大值和最小值.
分析 (1)利用基本不等式可得g(x)=$\frac{1}{2}$(x+$\frac{1-t}{x}$)≥$\sqrt{1-t}$;再由二次函数知h(x)=$\sqrt{{x}^{2}-2x+2+t}$=$\sqrt{(x-1)^{2}+1+t}$≥$\sqrt{1+t}$;从而可得$\sqrt{1-t}$,$\sqrt{1+t}$是方程-x2+ax+b=0的两个根;借助根与系数的关系可化简得b=1-$\frac{{a}^{2}}{2}$;再由-x2+ax+b=0的两根分别在(1,$\sqrt{2}$),(0,1)上可得$\sqrt{2}$<a<2;
(2)化简f(x)=-x3+ax2+(1-$\frac{{a}^{2}}{2}$)x,再求导f′(x)=-3x2+2ax+1-$\frac{{a}^{2}}{2}$,从而可判断函数f′(x)在区间[1,2]上单调递减,函数f(x)在[1,2]上单调递减;从而求函数f(x)在区间[1,2]上的最值.
解答 解:(1)∵0<t<1,x>0,
∴g(x)=$\frac{1}{2}$(x+$\frac{1-t}{x}$)≥$\sqrt{1-t}$;
(当且仅当x=$\frac{1-t}{x}$,即x=$\sqrt{1-t}$时,等号成立)
h(x)=$\sqrt{{x}^{2}-2x+2+t}$=$\sqrt{(x-1)^{2}+1+t}$,
故当x=1时,[h(x)]min=$\sqrt{1+t}$;
∵0<t<1,
∴1<$\sqrt{1+t}$<$\sqrt{2}$,0<$\sqrt{1-t}$<1,
∵f(x)=-x3+ax2+bx=x(-x2+ax+b),
结合题意可知:$\sqrt{1-t}$,$\sqrt{1+t}$是方程-x2+ax+b=0的两个根,
∴$\sqrt{1-t}$+$\sqrt{1+t}$=a,$\sqrt{1-t}$$\sqrt{1+t}$=-b;
∴a2=2+2$\sqrt{1-t}$$\sqrt{1+t}$=2-2b;
∴b=1-$\frac{{a}^{2}}{2}$;
再由-x2+ax+b=0的两根分别在(1,$\sqrt{2}$),(0,1)上知,
$\left\{\begin{array}{l}{b=1-\frac{{a}^{2}}{2}<0}\\{-1+a+1-\frac{{a}^{2}}{2}>0}\\{-2+\sqrt{2}a+1-\frac{{a}^{2}}{2}<0}\end{array}\right.$,
解得,$\sqrt{2}$<a<2;
故b=1-$\frac{{a}^{2}}{2}$,($\sqrt{2}$<a<2).
(2)由(1)得:f(x)=-x3+ax2+(1-$\frac{{a}^{2}}{2}$)x,
则f′(x)=-3x2+2ax+1-$\frac{{a}^{2}}{2}$,
∵$\sqrt{2}$<a<2,
∴二次函数f′(x)=-3x2+2ax+1-$\frac{{a}^{2}}{2}$的图象开口向下,
对称轴为x=$\frac{a}{3}$<$\frac{2}{3}$;
∴函数f′(x)在区间[1,2]上单调递减,
又f′(1)=-3+2a+1-$\frac{{a}^{2}}{2}$=-$\frac{1}{2}$(a-2)2<0,
∴当x∈[1,2]时,f′(x)≤f′(1)<0,
∴函数f(x)在[1,2]上单调递减;
∴函数f(x)的最大值为f(1)=a-$\frac{{a}^{2}}{2}$;最小值为f(2)=-a2+4a-6.
点评 本题考查了基本不等式在求最值中的应用,二次函数配方法求最值,根与系数的关系应用,同时考查了导数的综合应用及学生化简与运算的能力,属于难题.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案| 日期 | 1月1日 | 2月28日 | 3月21日 | 4月27日 | 5月6日 | 6月21日 | 8月13日 | 9月20日 | 10月25日 | 12月21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 268 | 298 | 355 |
| 白昼时间y(小时) | 5.6 | 10.2 | 12.4 | 16.4 | 17.3 | 19.4 | 16.4 | 12.4 | 8.5 | 5.4 |
(2)用(1)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
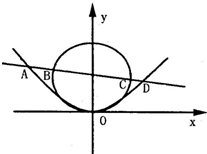 如图,过抛物线y=$\frac{1}{8}$x2的焦点且斜率为-$\frac{1}{2}$的直线交抛物线与圆x2+(y-2)2=4分别于A、D和B、C四点,则|AB|•|CD|=( )
如图,过抛物线y=$\frac{1}{8}$x2的焦点且斜率为-$\frac{1}{2}$的直线交抛物线与圆x2+(y-2)2=4分别于A、D和B、C四点,则|AB|•|CD|=( )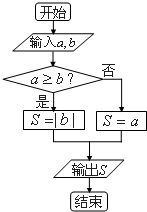 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为2.
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为2.