题目内容
12.已知一个正方形的边长为1cm,以它的对角线为边作一个新的正方形,再以新的正方形的对角线为边作正方形,这样继续下去,共作36个正方形,那么第六个正方形(包括已知正方形)的边长是$(\sqrt{2})^{5}$,这6个正方形的面积和是63.分析 由题意和等比数列的定义可知:各个、面积依次正方形的边长构成一个等比数列,分别求出首项和公比,利用等比数列的通项公式、前n项和公式求出答案.
解答 解:由题意得,各个正方形的边长构成一个等比数列,首项是1、公比是$\sqrt{2}$,
所以第六个正方形的边长是1×$(\sqrt{2})^{5}$=$(\sqrt{2})^{5}$,
各个正方形的面积依次依次构成一个等比数列,首项是1、公比是2,
所以这6个正方形的面积和S=$\frac{1-{2}^{6}}{1-2}$=63,
故答案为:$(\sqrt{2})^{5}$;63.
点评 本题考查等比数列的实际应用,以及等比数列的定义、通项公式、前n项和公式,属于中档题.

练习册系列答案
相关题目
2.某程序框如图所示,改程序运行后输出的结果是( )


| A. | -20 | B. | -15 | C. | -12 | D. | -10 |
3.已知函数f(x)是R上的单调增函数且为奇函数,数列{an}是等差数列,a11>0,则f(a9)+f(a11)+f(a13)的值( )
| A. | 恒为正数 | B. | 恒为负数 | C. | 恒为0 | D. | 可正可负 |
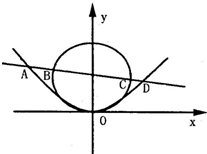 如图,过抛物线y=$\frac{1}{8}$x2的焦点且斜率为-$\frac{1}{2}$的直线交抛物线与圆x2+(y-2)2=4分别于A、D和B、C四点,则|AB|•|CD|=( )
如图,过抛物线y=$\frac{1}{8}$x2的焦点且斜率为-$\frac{1}{2}$的直线交抛物线与圆x2+(y-2)2=4分别于A、D和B、C四点,则|AB|•|CD|=( )