题目内容
如右图所示,已知 是等腰直角三角形,
是等腰直角三角形, ,
, 则
则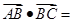 (***)
(***)
| A.4 | B. | C.2 | D.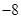 |
B
解析试题分析:根据题意,由于已知 是等腰直角三角形,
是等腰直角三角形, ,
, 则
则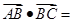 表示的为向量
表示的为向量 长度乘以
长度乘以 在
在 的投影的积,而结合三角形是等腰可知
的投影的积,而结合三角形是等腰可知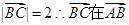 上的投影为负数,因为夹角为钝角,且长度为
上的投影为负数,因为夹角为钝角,且长度为 ,那么利用数量积的几何意义,可知结论为-4,故选B.
,那么利用数量积的几何意义,可知结论为-4,故选B.
考点:向量的数量积几何意义
点评:解决的关键是理解向量的数量积的几何意义能结合特殊的三角形来求解值,属于基础题。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知△ABC为等边三角形, ,设点P,Q满足
,设点P,Q满足 ,
, ,
, ,若
,若 ,则
,则 ( )
( )
A. | B. | C.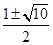 | D. |
设点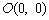 、
、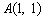 、
、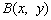 且
且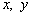 满足
满足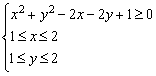 ,则
,则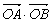 取得最小值时,点B的个数是( )
取得最小值时,点B的个数是( )
| A.1个 | B.2个 | C.3个 | D.无数个 |
已知向量 ,
, ,若
,若 ,则实数x的值为
,则实数x的值为
| A.1 | B. | C. | D. |
若 ,
, 且(
且( )⊥
)⊥ ,则
,则 与
与 的夹角是 ( )
的夹角是 ( )
A.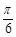 | B. | C. | D. |
平行六面体 中,设
中,设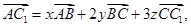 则
则 ( )
( )
| A.1 | B. | C. | D.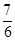 |
 中,
中, ,
, 分别为
分别为 中点,
中点, 为
为 上任意一点,实数
上任意一点,实数 满足
满足 ,设
,设 的面积分别为
的面积分别为 ,
, 取得最大值时,
取得最大值时, 的值为( )
的值为( )



 ,下列结论中正确的是 ( )
,下列结论中正确的是 ( ) 、
、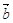 满足:
满足: ,
, ,
, ,则
,则 ________
________