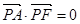题目内容
设双曲线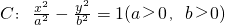 ,点A、B分别为双曲线C实轴的左端点和虚轴的上端点,点F1、F2分别为双曲线C的左、右焦点,点M、N是双曲线C的右支上不同两点,点Q为线段MN的中点.已知在双曲线C上存在一点P,使得
,点A、B分别为双曲线C实轴的左端点和虚轴的上端点,点F1、F2分别为双曲线C的左、右焦点,点M、N是双曲线C的右支上不同两点,点Q为线段MN的中点.已知在双曲线C上存在一点P,使得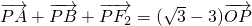 .
.
(Ⅰ)求双曲线C的离心率;
(Ⅱ)设a为正常数,若点Q在直线y=2x上,求直线MN在y轴上的截距的取值范围.
解:(Ⅰ)由题设,点A(-a,0),B(0,b),F1(-c,0),F2(c,0),其中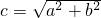 .(1分)
.(1分)
因为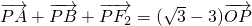 ,则
,则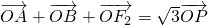 .
.
设点P(x0,y0)
,则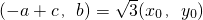 ,所以
,所以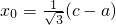 ,
, .(3分)
.(3分)
因为点P在双曲线 上,所以,即(c-a)2=4a2.(4分)
上,所以,即(c-a)2=4a2.(4分)
因为c>a,所以c-a=2a,即c=3a,故离心率 .(6分)
.(6分)
(Ⅱ)由(Ⅰ)知c=3a,则b2=c2-a2=8a2.(7分)
若MN⊥x轴,则Q在x轴上,不合题意.
设直线MN的方程为y=kx+m,代入 ,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.(*)(9分)
,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.(*)(9分)
若k2=8,则MN与双曲线C的渐近线平行,不合题意.
设点M(x1,y1),N(x2,y2),Q(x0,y0),则 ,
,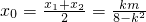 ,
, .(10分)
.(10分)
若点Q在直线y=2x上,则 .
.
因为点M、N在双曲线的右支上,所以m≠0,从而k=4.(11分)
此时,方程(*)可化为8x2+8mx+m2+8a2=0.
由△=82m2-4×8(m2+8a2)>0,得m2>8a2.(12分)
又M、N在双曲线C的右支上,则x1+x2=-m>0,所以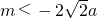 .
.
故直线MN在y轴上的截距的取值范围是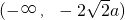 .(13分)
.(13分)
分析:(Ⅰ)由题设知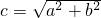 .
.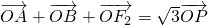 .设点P(x0,y0)
.设点P(x0,y0) ,则有
,则有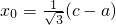 ,
, .由此推导出c=3a,可得离心率;
.由此推导出c=3a,可得离心率;
(Ⅱ)由题意知c=3a,则b2=c2-a2=8a2.若MN⊥x轴,则Q在x轴上,不合题意.设直线MN的方程为y=kx+m,代入 ,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.若k2=8,则MN与双曲线C的渐近线平行,不合题意.设点M(x1,y1),N(x2,y2),Q(x0,y0),由根与系数的关系能够推导出直线MN在y轴上的截距的取值范围.
,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.若k2=8,则MN与双曲线C的渐近线平行,不合题意.设点M(x1,y1),N(x2,y2),Q(x0,y0),由根与系数的关系能够推导出直线MN在y轴上的截距的取值范围.
点评:本题考查直线和圆锥曲线的位置关系,解题时要注意公式的灵活运用.
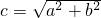 .(1分)
.(1分)因为
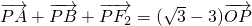 ,则
,则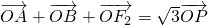 .
.设点P(x0,y0)

,则
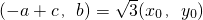 ,所以
,所以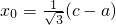 ,
, .(3分)
.(3分)因为点P在双曲线
 上,所以,即(c-a)2=4a2.(4分)
上,所以,即(c-a)2=4a2.(4分)因为c>a,所以c-a=2a,即c=3a,故离心率
 .(6分)
.(6分)(Ⅱ)由(Ⅰ)知c=3a,则b2=c2-a2=8a2.(7分)
若MN⊥x轴,则Q在x轴上,不合题意.
设直线MN的方程为y=kx+m,代入
 ,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.(*)(9分)
,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.(*)(9分)若k2=8,则MN与双曲线C的渐近线平行,不合题意.
设点M(x1,y1),N(x2,y2),Q(x0,y0),则
 ,
,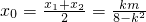 ,
, .(10分)
.(10分)若点Q在直线y=2x上,则
 .
.因为点M、N在双曲线的右支上,所以m≠0,从而k=4.(11分)
此时,方程(*)可化为8x2+8mx+m2+8a2=0.
由△=82m2-4×8(m2+8a2)>0,得m2>8a2.(12分)
又M、N在双曲线C的右支上,则x1+x2=-m>0,所以
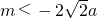 .
.故直线MN在y轴上的截距的取值范围是
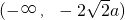 .(13分)
.(13分)分析:(Ⅰ)由题设知
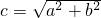 .
.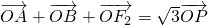 .设点P(x0,y0)
.设点P(x0,y0) ,则有
,则有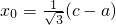 ,
, .由此推导出c=3a,可得离心率;
.由此推导出c=3a,可得离心率;(Ⅱ)由题意知c=3a,则b2=c2-a2=8a2.若MN⊥x轴,则Q在x轴上,不合题意.设直线MN的方程为y=kx+m,代入
 ,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.若k2=8,则MN与双曲线C的渐近线平行,不合题意.设点M(x1,y1),N(x2,y2),Q(x0,y0),由根与系数的关系能够推导出直线MN在y轴上的截距的取值范围.
,得8x2-(kx+m)2=8a2,即(8-k2)x2-2kmx-m2-8a2=0.若k2=8,则MN与双曲线C的渐近线平行,不合题意.设点M(x1,y1),N(x2,y2),Q(x0,y0),由根与系数的关系能够推导出直线MN在y轴上的截距的取值范围.点评:本题考查直线和圆锥曲线的位置关系,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
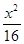
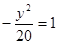 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,