题目内容
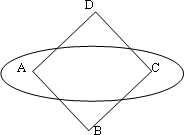
 如图,椭圆以边长为1的正方形ABCD的对角顶点A,C为焦点,且经过各边的中点,试建立适当的坐标系,求椭圆的方程.
如图,椭圆以边长为1的正方形ABCD的对角顶点A,C为焦点,且经过各边的中点,试建立适当的坐标系,求椭圆的方程.
分析:建立如图所示的坐标系,写出A、C、D、E的坐标,利用椭圆的定义及标准方程的形式,待定系数法求椭圆的方程.
解答: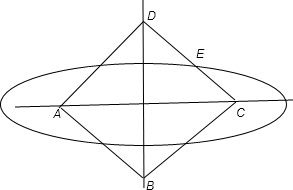 解:如图所示:以点A,C所在直线为x轴,以线段AC的中垂线为y轴,建立平面直角坐标系,
解:如图所示:以点A,C所在直线为x轴,以线段AC的中垂线为y轴,建立平面直角坐标系,
则A(-
,0)、C(
,0),D(0,
),
故CD的中点 E(
,
),
∵E在椭圆上,由椭圆的定义,
得EA+EC=2a=
+
=
+
=
,
∴a=
.
又 c=
,∴b2=a2-c2=
,∴椭圆的方程为:
+
=1.
 解:如图所示:以点A,C所在直线为x轴,以线段AC的中垂线为y轴,建立平面直角坐标系,
解:如图所示:以点A,C所在直线为x轴,以线段AC的中垂线为y轴,建立平面直角坐标系,则A(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故CD的中点 E(
| ||
| 4 |
| ||
| 4 |
∵E在椭圆上,由椭圆的定义,
得EA+EC=2a=
(
|
(-
|
=
| ||
| 2 |
| 1 |
| 2 |
1+
| ||
| 2 |
∴a=
1+
| ||
| 4 |
又 c=
| ||
| 2 |
| ||
| 8 |
| 8x2 | ||
3+
|
| 32y2 | ||
3-
|
点评:本题考查利用椭圆的定义,用待定系数法求椭圆的标准方程的方法,属于中档题.

练习册系列答案
相关题目