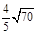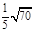题目内容
如图所示,在三棱锥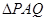 中,
中,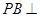 平面
平面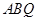 ,
,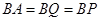 ,
,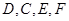 分别是
分别是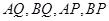 的中点,
的中点,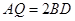 ,
,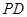 与
与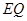 交于
交于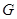 ,
,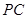 与
与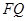 交于点
交于点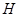 ,连接
,连接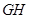 。
。
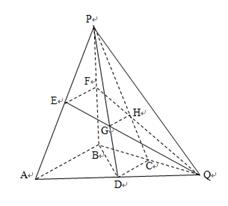
(Ⅰ)求证: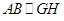 ;
;
(Ⅱ)求二面角 的余弦值。
的余弦值。
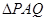 中,
中,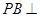 平面
平面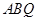 ,
,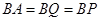 ,
,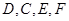 分别是
分别是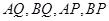 的中点,
的中点,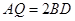 ,
,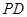 与
与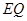 交于
交于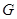 ,
,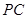 与
与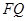 交于点
交于点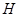 ,连接
,连接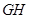 。
。
(Ⅰ)求证:
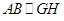 ;
;(Ⅱ)求二面角
 的余弦值。
的余弦值。(Ⅰ)见解析 (Ⅱ)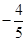
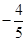
解法一 (Ⅰ)在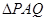 中,
中,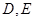 分别是
分别是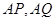 的中点,则
的中点,则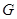 是
是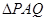 的重心,
的重心,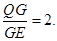
同理,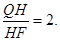 所以
所以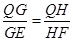 ,因此
,因此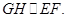
又因为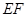 是
是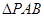 的中位线,所以
的中位线,所以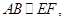
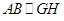 .
.
(Ⅱ)解法1 因为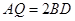 ,所以
,所以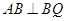 ,又
,又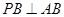 ,
,
所以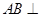 平面
平面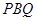 ,
,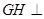 平面
平面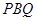 ,
,
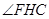 为二面角
为二面角 的平面角,
的平面角,
不妨设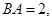 由三角形知识可得
由三角形知识可得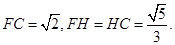
由余弦定理得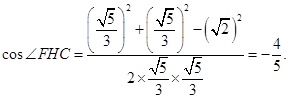
解法2分别以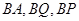 所在直线为
所在直线为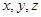 轴建立空间直角坐标系,不妨设
轴建立空间直角坐标系,不妨设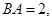 则
则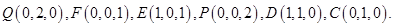
设平面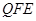 的法向量为
的法向量为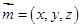 ,则
,则
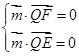 ,所以
,所以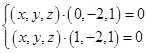 ,令
,令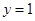 得
得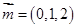
同理求得平面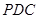 的一个法向量为
的一个法向量为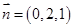 ,
,
因此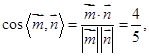
由图形可知二面角 的余弦值为
的余弦值为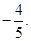
解法二(Ⅰ)证明:因为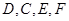 分别是
分别是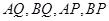 的中点,
的中点,
所以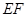 ∥
∥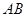 ,
,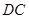 ∥
∥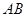 ,所以
,所以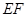 ∥
∥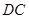 ,
,
又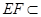 平面
平面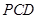 ,
,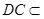 平面
平面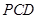 ,
,
所以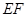 ∥平面
∥平面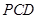 ,
,
又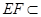 平面
平面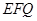 ,平面
,平面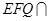 平面
平面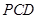
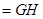 ,
,
所以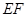 ∥
∥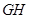 ,
,
又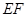 ∥
∥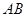 ,
,
所以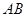 ∥
∥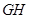 .
.
(Ⅱ)解法一:在△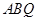 中,
中, 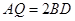 ,
,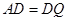 ,
,
所以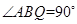 ,即
,即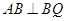 ,因为
,因为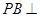 平面
平面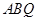 ,所以
,所以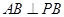 ,
,
又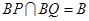 ,所以
,所以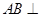 平面
平面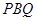 ,由(Ⅰ)知
,由(Ⅰ)知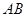 ∥
∥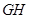 ,
,
所以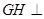 平面
平面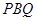 ,又
,又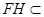 平面
平面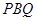 ,所以
,所以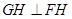 ,同理可得
,同理可得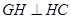 ,
,
所以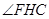 为二面角
为二面角 的平面角,设
的平面角,设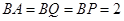 ,连接
,连接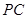 ,
,
在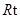 △
△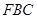 中,由勾股定理得,
中,由勾股定理得,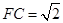 ,
,
在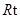 △
△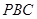 中,由勾股定理得,
中,由勾股定理得,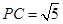 ,
,
又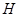 为△
为△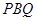 的重心,所以
的重心,所以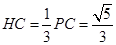
同理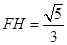 ,
,
在△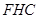 中,由余弦定理得
中,由余弦定理得 ,
,
即二面角 的余弦值为
的余弦值为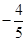 .
.
解法二:在△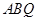 中,
中,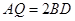 ,
,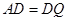 ,
,
所以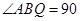 ,又
,又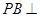 平面
平面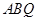 ,所以
,所以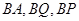 两两垂直,
两两垂直,
以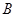 为坐标原点,分别以
为坐标原点,分别以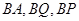 所在直线为
所在直线为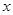 轴,
轴,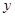 轴,
轴,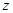 轴,建立如图所示的空间直角坐标系,设
轴,建立如图所示的空间直角坐标系,设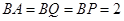 ,则
,则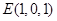 ,
,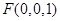 ,
,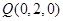 ,
,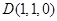 ,
,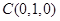
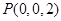 ,,所以
,,所以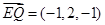 ,
,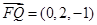 ,
,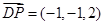 ,
,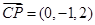 ,
,
设平面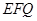 的一个法向量为
的一个法向量为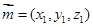 ,
,
由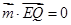 ,
,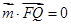 ,
,
得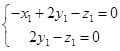
取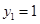 ,得
,得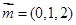 .
.
设平面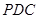 的一个法向量为
的一个法向量为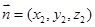
由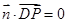 ,
,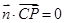 ,
,
得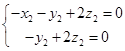
取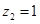 ,得
,得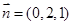 .所以
.所以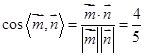
因为二面角 为钝角,所以二面角
为钝角,所以二面角 的余弦值为
的余弦值为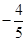 .
.
【考点定位】本题考查了空间直线的位置关系的判定和二面角的求法,考查了空间想象能力、推理论证能力和运算能力。第一问主要涉及平面几何的图形性质,中点形成的平行线是常考点之一,论证较为简单。第二问有两种方法可以解决,因图形结构的简洁性,推理论证较为简单,而利用空间向量运算求解二面角就相对复杂了.
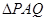 中,
中,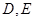 分别是
分别是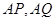 的中点,则
的中点,则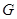 是
是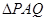 的重心,
的重心,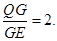
同理,
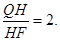 所以
所以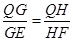 ,因此
,因此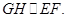
又因为
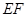 是
是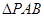 的中位线,所以
的中位线,所以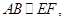
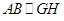 .
.(Ⅱ)解法1 因为
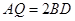 ,所以
,所以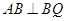 ,又
,又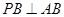 ,
,所以
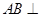 平面
平面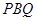 ,
,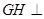 平面
平面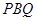 ,
,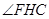 为二面角
为二面角 的平面角,
的平面角,不妨设
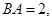 由三角形知识可得
由三角形知识可得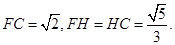
由余弦定理得
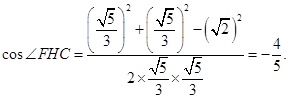
解法2分别以
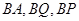 所在直线为
所在直线为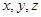 轴建立空间直角坐标系,不妨设
轴建立空间直角坐标系,不妨设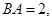 则
则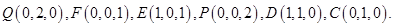
设平面
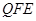 的法向量为
的法向量为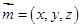 ,则
,则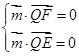 ,所以
,所以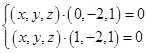 ,令
,令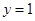 得
得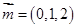
同理求得平面
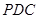 的一个法向量为
的一个法向量为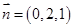 ,
,因此
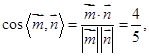
由图形可知二面角
 的余弦值为
的余弦值为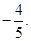
解法二(Ⅰ)证明:因为
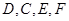 分别是
分别是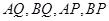 的中点,
的中点,所以
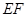 ∥
∥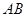 ,
,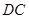 ∥
∥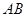 ,所以
,所以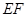 ∥
∥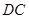 ,
,又
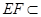 平面
平面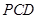 ,
,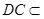 平面
平面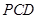 ,
,所以
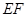 ∥平面
∥平面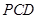 ,
,又
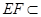 平面
平面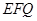 ,平面
,平面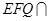 平面
平面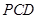
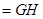 ,
,所以
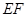 ∥
∥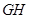 ,
,又
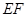 ∥
∥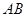 ,
,所以
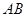 ∥
∥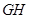 .
.(Ⅱ)解法一:在△
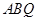 中,
中, 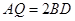 ,
,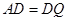 ,
,所以
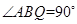 ,即
,即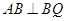 ,因为
,因为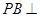 平面
平面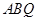 ,所以
,所以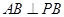 ,
,又
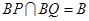 ,所以
,所以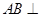 平面
平面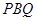 ,由(Ⅰ)知
,由(Ⅰ)知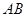 ∥
∥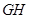 ,
,所以
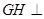 平面
平面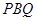 ,又
,又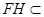 平面
平面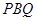 ,所以
,所以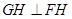 ,同理可得
,同理可得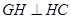 ,
,所以
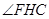 为二面角
为二面角 的平面角,设
的平面角,设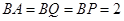 ,连接
,连接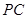 ,
,在
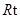 △
△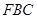 中,由勾股定理得,
中,由勾股定理得,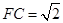 ,
,在
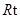 △
△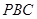 中,由勾股定理得,
中,由勾股定理得,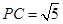 ,
,又
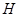 为△
为△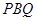 的重心,所以
的重心,所以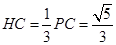
同理
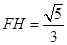 ,
,在△
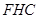 中,由余弦定理得
中,由余弦定理得 ,
,即二面角
 的余弦值为
的余弦值为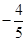 .
.解法二:在△
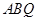 中,
中,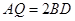 ,
,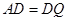 ,
,所以
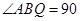 ,又
,又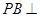 平面
平面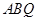 ,所以
,所以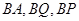 两两垂直,
两两垂直,以
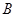 为坐标原点,分别以
为坐标原点,分别以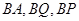 所在直线为
所在直线为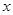 轴,
轴,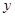 轴,
轴,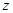 轴,建立如图所示的空间直角坐标系,设
轴,建立如图所示的空间直角坐标系,设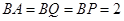 ,则
,则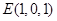 ,
,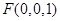 ,
,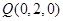 ,
,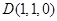 ,
,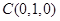
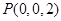 ,,所以
,,所以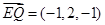 ,
,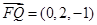 ,
,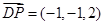 ,
,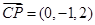 ,
,设平面
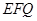 的一个法向量为
的一个法向量为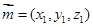 ,
,由
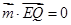 ,
,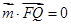 ,
,得
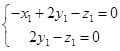
取
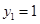 ,得
,得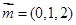 .
.设平面
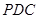 的一个法向量为
的一个法向量为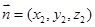
由
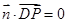 ,
,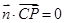 ,
,得
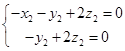
取
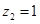 ,得
,得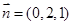 .所以
.所以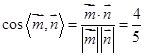
因为二面角
 为钝角,所以二面角
为钝角,所以二面角 的余弦值为
的余弦值为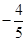 .
.【考点定位】本题考查了空间直线的位置关系的判定和二面角的求法,考查了空间想象能力、推理论证能力和运算能力。第一问主要涉及平面几何的图形性质,中点形成的平行线是常考点之一,论证较为简单。第二问有两种方法可以解决,因图形结构的简洁性,推理论证较为简单,而利用空间向量运算求解二面角就相对复杂了.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 中,
中,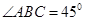 ,
,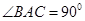 ,
,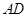 是
是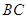 上的高,沿
上的高,沿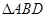 折起,使
折起,使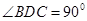 .
.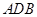 ⊥平面
⊥平面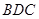 ;
;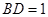 ,求三棱锥
,求三棱锥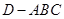 的表面积.
的表面积.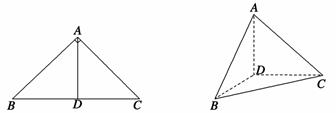
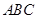 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
 平面
平面 ;
; 的平面角的余弦值.
的平面角的余弦值.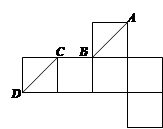
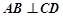 B.
B. 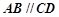
 D. AB与CD相交
D. AB与CD相交 中,四边形
中,四边形 是正方形,
是正方形, 平面
平面 ∥
∥

 与
与 所成角的余弦值;
所成角的余弦值; 平面
平面 ;
; 的正切值。
的正切值。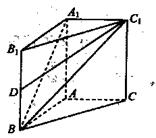
 的对棱
的对棱 、
、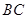 成
成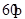 的角,且
的角,且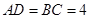 ,平行于
,平行于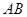 、
、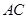 、
、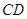 、
、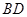 于
于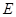 、
、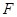 、
、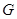 、
、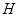 .
.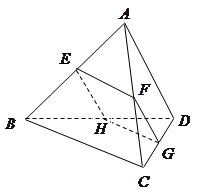
 为平行四边形;
为平行四边形;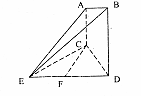
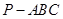 中,
中,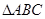 是底面,
是底面,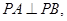
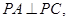
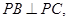 且这四个顶点都在半径为2的球面上,
且这四个顶点都在半径为2的球面上,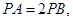 则这个三棱锥的三个侧棱长的和的最大值为( )
则这个三棱锥的三个侧棱长的和的最大值为( )