题目内容
已知函数f(x)=ax3+bx2+cx+d．在x=0处取得极值，曲线y=f(x)的图像过原点和点P(-1，2)，且在P点处的切线与直线3x+y=0平行．(1)求f(x)的表达式；
(2)若函数f(x)在[2m-1，m+1]上是递增函数；求m的取值范围．
解：(1)∵f(x)=ax3+bx2+cx+d
∴f′(x)=3ax2+2bx+c
依题意：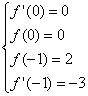
即
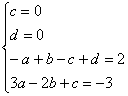
∴a=1 b=3 c=0 d=0
故f(x)=x3+3x2
(2)f′(x)=3x2+6x
令f′(x)＞0 则3x2+6x＞0 ∴x＞0或x＜-2
∴f(x)在递增区间为(-∞，-2]或[0，+∞)
又f(x)在[2m-1，m+1]上为递增函数
∴
或
m≤-3或
≤m＜2
练习册系列答案
相关题目
已知函数f(x)=a-
，若f（x）为奇函数，则a=（ ）
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |