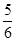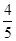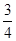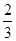题目内容
在平面直角坐标系中,定点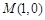 ,两动点
,两动点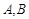 在双曲线
在双曲线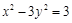 的右支上,则
的右支上,则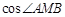 的最小值是( )
的最小值是( )
A.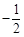 | B.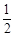 | C.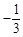 | D.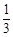 |
D
解析试题分析:由图可知,当直线MA、MB与双曲线相切时,∠AMB最大,此时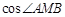 最小,设过点M的双曲线切线方程为:
最小,设过点M的双曲线切线方程为: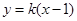 代入
代入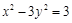 整理得,
整理得,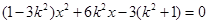 ,则△=
,则△=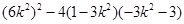 =0,解得
=0,解得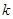 =
=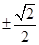 ,即
,即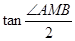 =
=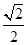 ,∴
,∴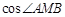 =
= =
=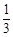 ,故选D.
,故选D.
考点:1.直线与双曲线的位置关系;2.二倍角公式;3.数形结合思想;4.转化与化归思想

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知圆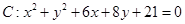 ,抛物线
,抛物线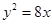 的准线为L,设抛物线上任意一点
的准线为L,设抛物线上任意一点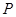 到直线L的距离为
到直线L的距离为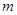 ,则
,则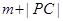 的最小值为
的最小值为
| A.5 | B.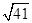 | C.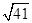 -2 -2 | D.4 |
抛物线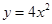 的焦点到准线的距离是( )
的焦点到准线的距离是( )
| A.2 | B.4 | C.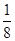 | D.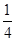 |
抛物线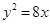 上到其焦点
上到其焦点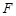 距离为5的点有( )
距离为5的点有( )
| A.0个 | B.1个 | C.2个 | D.4个 |
过点(0,1)与双曲线 仅有一个公共点的直线共有( )
仅有一个公共点的直线共有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
已知对 ,直线
,直线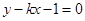 与椭圆
与椭圆 恒有公共点,则实数
恒有公共点,则实数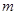 的取值范围是
的取值范围是
| A.(0, 1) | B.(0,5) | C.[1,5) | D.[1,5)∪(5,+∞) |
若双曲线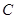 :
: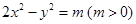 与抛物线
与抛物线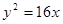 的准线交于
的准线交于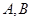 两点,且
两点,且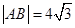 ,则
,则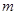 的值是( )
的值是( )
A.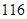 | B.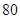 . . | C.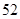 | D.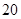 |
已知椭圆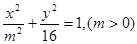 和双曲线
和双曲线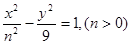 有相同的焦点
有相同的焦点 ,点
,点 为椭圆和双曲线的一个交点,则
为椭圆和双曲线的一个交点,则 的值为( )
的值为( )
| A.16 | B.25 | C.9 | D.不为定值 |
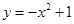 的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P, 则点P落在
的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P, 则点P落在 AOB内的概率是( )
AOB内的概率是( )