Question

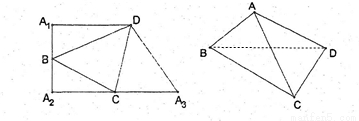
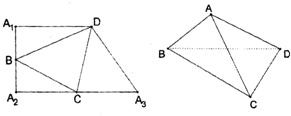在直角梯形A₁A₂A₃D中，A₁A₂⊥A₁D，A₁A₂⊥A₂A₃，且B，C分别是边A₁A₂，A₂A₃上的一点，沿线段BC，CD，DB分别将△BCA₂，△CDA₃，△DBA₁
翻折上去恰好使A₁，A₂，A₃重合于一点A
（Ⅰ） 求证：AB⊥CD；
（Ⅱ）已知A₁D=10，A₁A₂=8，，试求：（1）四面体ABCD内切球的表面积；（2）二面角A-BC-D的余弦值．

Answer 1

分析：（I）先根据翻折前后在同一个面上的位置故选及度量故选不变，得到）∠BAC=∠BAD=

π

2

，利用线面垂直的判定定理及线面垂直的性质得到AB⊥CD
（II）（1）将三棱锥的体积用内切球的半径表示，利用三棱锥的体积公式求出其体积，进一步求出内切球的半径，利用球的表面积公式求出其表面积．
（2）建立空间直角坐标系，利用面的法向量垂直面内的两个相交向量，列出方程组求出平面BCD的法向量，利用向量的数量积求出两个法向量所成角的余弦值，再根据二面角与法向量所成角的关系得到二面角A-BC-D的余弦值．

解答：解：（I）∠BAC=∠BAD=

π

2

∴BA⊥面ACD
∴AB⊥CD
（II）（1）VABCD=

1

3

S表•r
∴r= 

3VABCD

S表

=

3VABCD

S梯形A1A2A3A4

=

( 1 2 ×8×8)×4

1 2 (10+16)×8

=

16

13

∴S球=4πr2=

1024π

169

（2）以AC 所在的直线为y轴AB所在的直线为y轴建立空间直角坐标系，则
（0，0，0），B（0，0，4），C（0，8，0）D（8，6，0）
∴平面ABC的法向量为

n1

=(1，0，0)
设平面BCD的法向量为

n2

=(1，x，y)
又

BC

=(0，8，-4)，

BD

=(8，6，-4)
∴

8x-4y=0 8+6x-4y=0

解得

x=4 y=8

∴

n2

=(1，4，8)
∴cos＜

n1

，

n2

＞=

n1 • n2

| n1 || n2 |

设二面角A-BC-D为α
∴cosα=

1

9

点评：解决此类问题的关键是熟练掌握几何体的结构特征，根据几何体的结构特征得到空间中的线面关系，进而建立坐标系利用向量的有关运算解决空间角、空间距离与体积等问题