题目内容
函数y=xe-x,x∈[0,4]的最大值是_________
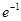
解析试题分析:求出f(x)的导函数,令导函数等于0求出x的值,利用x的值分区间讨论导函数的正负,得到函数的单调区间,根据函数的增减性进而得到函数的极大值。解:令f′(x)=(1-x)e-x=0,解得x=1,所以当x变化时,f(x)和f′(x)的变化情况如图所示: 
所以函数的极大值为f(1)=e-1.即为最大值为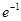
考点:导函数的正负得出函数的单调区间
点评:此题考查学生会利用导函数的正负得出函数的单调区间,并根据函数的增减性得到函数的极值,是一道综合题

练习册系列答案
相关题目
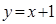 与曲线
与曲线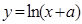 相切,则
相切,则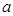 的值为 .
的值为 .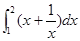 =__________
=__________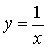 和
和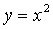 在它们交点处的两条切线与
在它们交点处的两条切线与 轴所围成的三角形面积是 .
轴所围成的三角形面积是 . ,若函数
,若函数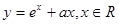 有大于零的极值点,则
有大于零的极值点,则 的取值范围是
的取值范围是  ,对任意
,对任意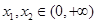 ,不等式
,不等式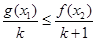 恒成立,则正数
恒成立,则正数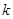 的取值范围是
的取值范围是 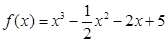 ,当
,当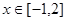 时,
时,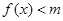 恒成立,则实数
恒成立,则实数 的取值范围为 .
的取值范围为 . 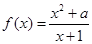 在
在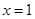 处取极值,则
处取极值,则 .
. 有极大值和极小值,则
有极大值和极小值,则 的取值范围是__ .
的取值范围是__ .