题目内容
设函数 ,对任意
,对任意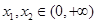 ,不等式
,不等式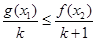 恒成立,则正数
恒成立,则正数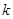 的取值范围是
的取值范围是
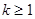
解析试题分析:因为,当x>0时,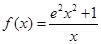 =e2x+
=e2x+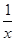 ≥2
≥2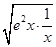 =2e
=2e
所以x1∈(0,+∞)时,函数f(x1)有最小值2e
因为,g(x)=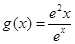 ,所以,
,所以,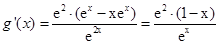
当x<1时,g′(x)>0,则函数g(x)在(0,1)上单调递增
当x>1时,g′(x)<0,则函数在(1,+∞)上单调递减
∴x=1时,函数g(x)有最大值g(1)=e
则有x1、x2∈(0,+∞),f(x1)min=2e>g(x2)max=e
又因为,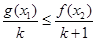 恒成立且k>0
恒成立且k>0
所以,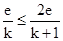 ,所以,k≥1,故答案为k≥1。
,所以,k≥1,故答案为k≥1。
考点:本题主要考查利用导数研究函数的单调性,均值定理的应用。
点评:中档题,解答本题的关键是认识到,由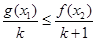 恒成立且k>0,
恒成立且k>0,
确定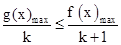 ,将问题转化成求函数的最值问题。本题难度较大。
,将问题转化成求函数的最值问题。本题难度较大。

练习册系列答案
相关题目
 满足
满足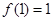 ,
,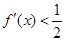 ,则不等式
,则不等式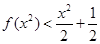 的解集为______.
的解集为______.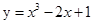 在点(1,f(x))处的切线方程为
在点(1,f(x))处的切线方程为 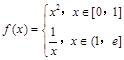 (其中
(其中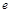 为自然对数的底数),则
为自然对数的底数),则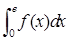 = .
= . 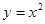 与
与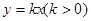 的图像所围成的图形的面积为
的图像所围成的图形的面积为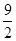 ,则
,则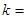 .
.
 的单调递增区间是 .
的单调递增区间是 .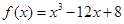 在区间
在区间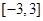 上的最大值与最小值分别为
上的最大值与最小值分别为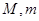 ,则
,则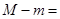 ___________.
___________. 单调递减区间是
单调递减区间是