题目内容
曲线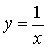
和
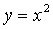在它们交点处的两条切线与
轴所围成的三角形面积是 .
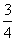
解析试题分析：先联立方程，求出两曲线交点，再分别对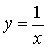和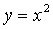求导，利用导数，求出两曲线在交点处的切线斜率，利用点斜式求出切线方程，找到两切线与x轴交点，最后用面积公式计算面积即可。解：曲线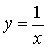和y=x2在它们的交点坐标是（1，1），两条切线方程分别是y=-x+2和y=2x-1，它们与x轴所围成的三角形的面积是．
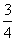考点：导数的几何意义
点评：本题考查了利用导数求切线斜率，属于导数的应用．应当掌握
练习册系列答案
相关题目
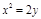上点
处的切线方程是 .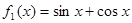
,记
, 
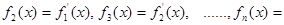
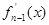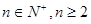).则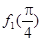
+
+…+
= 
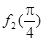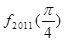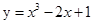在点（1,f(x)）处的切线方程为 
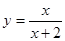在点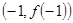
处的切线与直线
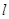垂直，则直线
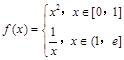(其中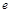
为自然对数的底数)，则
= . 
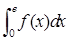的单调递增区间是 .
，当
时，
恒成立，则实数
的