题目内容
在△ABC中,已知2sinAcosB=sinC,那么△ABC一定是 三角形。
等腰三角形。
由2sinAcosB=sinC,知2sinAcosB=sin(A+B),
∴2sinAcosB=sinAcosB+cosAsinB. ∴cosAsinB-sinAcosB=0.
∴sin(B-A)=0. ∴B=A.另解:本题也可以借助正余弦定理来处理,但是稍微繁一点。
∴2sinAcosB=sinAcosB+cosAsinB. ∴cosAsinB-sinAcosB=0.
∴sin(B-A)=0. ∴B=A.另解:本题也可以借助正余弦定理来处理,但是稍微繁一点。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 周长为AC=3,4cos2A-cos2C=3。
周长为AC=3,4cos2A-cos2C=3。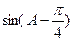 的值。
的值。 、
、 、
、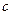 分别是
分别是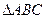 的三个内角
的三个内角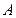 、
、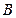 、
、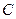 所对的边
所对的边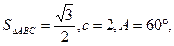 求
求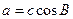 ,且
,且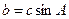 ,试判断
,试判断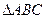 中,
中, 分别为三个内角A、B、C所对的边,设向量
分别为三个内角A、B、C所对的边,设向量
 ,若向量
,若向量 ,则角C的大小为 。
,则角C的大小为 。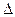 ABC三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为 .
ABC三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为 . 题
题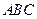 的内角
的内角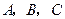 的对边分别为
的对边分别为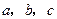 ,
,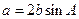 .(Ⅰ)求
.(Ⅰ)求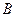 的大小;(Ⅱ)求
的大小;(Ⅱ)求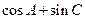 的取值范围.
的取值范围.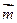 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量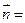 (2,0)所成角为
(2,0)所成角为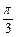 ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.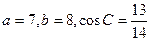 ,则最大角的余弦是( )
,则最大角的余弦是( )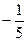
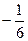
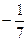
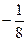
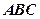 中,已知
中,已知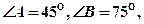 点
点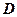 在
在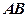 上,且
上,且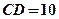 .若
.若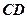 平分
平分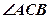 ,则
,则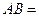 。
。