题目内容
一个单位有职工800人，期中具有高级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人.为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
| A．12,24,15,9 | B．9,12,12,7 |
| C．8,16,10,6 | D．8,15,12,5 |
D
解析试题分析：先求得比例，然后各层的总人数乘上这个比例，即得到样本中各层的人数．因为40：800=1：20，那么可知故各层中依次抽取的人数分别是
因此可得从上述各层中依次抽取的人数分别是8,15,12,5，选D.
考点：分层抽样
点评：本题主要考查分层抽样方法．属于基础题。
天天向上一本好卷系列答案
小学生10分钟应用题系列答案两个变量x，y与其线性相关系数r有下列说法
（1）若r>0，则x增大时，y也相应增大；
（2）若r<0，则x增大时，y也相应增大；
（3）若r＝1或r＝－1，则x与y的关系完全对应(有函数关系)，在散点图上各个散点均在一条直线上，其中正确的有 （ ）
| A．①② | B．②③ | C．①③ | D．①②③ |
某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图，则上班、下班时间行驶速度的中位数分别是（ ）
| A．2827.5 | B．2828.5 |
| C．2927.5 | D．2928.5 |
下表是
之间的一组数据，则
的线性回归直线必过点
A． | B． |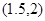
C． | D． |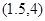
某班有50名同学，将其编为1、2、3、…、50号，并按编号从小到大平均分成5组．现用系统抽样方法，从该班抽取5名同学进行某项调查，若第1组抽取的学生编号为3，第2组抽取的学生编号为13，则第4组抽取的学生编号为
| A．14 | B．23 | C．33 | D．43 |
通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
算得，
附表：
 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
A．有99%以上的把握认为“爱好该项运动与性别有关”
B．有99%以上的把握认为“爱好该项运动与性别无关”
C．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”
D．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关”
某公司有员工49人，其中30岁以上的员工有14人，没超过30岁的员工有35人，为了解员工的健康情况，用分层抽样的方法抽一个容量为7的样本，其中30岁以上的员工应抽多少( )
| A．2人 | B．4人 | C．5人 | D．1人 |
如果在犯错误的概率不超过0.05的前提下说事件A和事件B有关系，那么算出的数据满足（ ）
A． | B． | C． | D． |
设有一个直线回归方程为y=2-1.5x,则变量x增加一个单位时 （ ）
| A．y平均增加1.5个单位 | B．y平均增加2个单位 |
| C．y平均减少1.5个单位 | D．y平均减少2个单位 |