题目内容
两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大;
(2)若r<0,则x增大时,y也相应增大;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,其中正确的有 ( )
| A.①② | B.②③ | C.①③ | D.①②③ |
C
解析试题分析:根据题意,由于(1)若r>0,则x增大时,y也相应增大;成立
对于(2)若r<0,则x增大时,y也相应增大;应该是减少,错误。
对于(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,正确,故答案选C.
考点:线性相关
点评:主要是考查了两个变量的线性相关性的概念,属于基础题。

某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和为( )
| A.117 | B.118 | C.118.5 | D.119.5 |
某校共有学生2000名,各年级男、女生人数如下表.已知在全校 学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为 .
| | 一年级 | 二年级 | 三年级 |
| 女生 | 373 |  |  |
| 男生 | 377 | 370 | 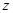 |
一个工厂有若干个车间,今采用分层抽样法从全厂某天的2000件产品中抽取一个容量为200的样本进行质量检查,若一车间这一天生产了80件产品,则从该车间抽取的产品件数为( )
| A. 2 | B.4 | C.6 | D.8 |
某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数为( )
| A.7 | B.8 | C.9 | D.10 |
有一个容量为 的样本,其频率分布直方图如图所示,据图估计,样本数据在
的样本,其频率分布直方图如图所示,据图估计,样本数据在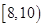 内的频数为
内的频数为
| A.38 | B.57 |
| C.76 | D.95 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长立形的面积等于其他10个小长方形的面积的和的 ,且样本容量为160,则中间一组有频数为 ( )
,且样本容量为160,则中间一组有频数为 ( )
| A.32 | B.0.2 | C.40 | D.0.25 |
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A.总偏差平方和 | B.残差平方和 | C.回归平方和 | D.相关指数R2 |
一个单位有职工800人,期中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
| A.12,24,15,9 | B.9,12,12,7 |
| C.8,16,10,6 | D.8,15,12,5 |