题目内容
设函数 ,集合
,集合 .
.
(1)若 ,求
,求 解析式。
解析式。
(2)若 ,且
,且 在
在 时的最小值为
时的最小值为 ,求实数
,求实数 的值。
的值。
【答案】
(1) ;(2)
;(2) 或
或 。
。
【解析】
试题分析:(1) ,变形为
,变形为 ,
,
由已知其两根分别为 ,由韦达定理可知:
,由韦达定理可知: ;
;
解出:
(2)由已知方程 有唯一根
有唯一根 ,所以
,所以 ,
,
解出 ,函数
,函数 ,其对称轴为
,其对称轴为 。下面分两种情况讨论:
。下面分两种情况讨论:
若 时,
时, ,解出
,解出
若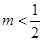 时,
时, ,解出
,解出 所以
所以 或
或
考点:本题主要考查一元二次方程根与系数的关系,二次函数的图象和性质。
点评:典型题,涉及二次函数的题目,往往需要借助于函数的图象解决问题,一般要考虑“开口方向,对称轴位置,与x轴交点情况,区间端点函数值”等。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
设函数f(x)=
,集合M={x|f(x)<0},P={x|f′(x)>0},若M?P,则实数a的取值范围是( )
| x-a |
| x-1 |
| A、(-∞,-1) |
| B、(0,1) |
| C、(1,+∞) |
| D、[1,+∞) |