题目内容
已知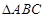 的顶点
的顶点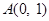 ,
,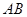 边上的中线
边上的中线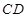 所在的直线方程为
所在的直线方程为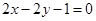 ,
,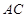 边上的高
边上的高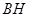 所在直线的方程为
所在直线的方程为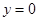 。
。
(1)求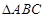 的顶点
的顶点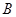 、
、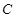 的坐标;
的坐标;
(2)若圆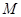 经过不同的三点
经过不同的三点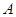 、
、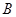 、
、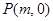 ,且斜率为
,且斜率为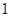 的直线与圆
的直线与圆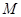 相切于点
相切于点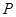 ,求圆
,求圆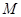 的方程;
的方程;
(3)问圆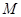 是否存在斜率为
是否存在斜率为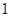 的直线
的直线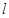 ,使
,使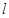 被圆
被圆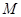 截得的弦为
截得的弦为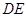 ,以
,以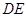 为直径的圆经过原点.若存在,写出直线
为直径的圆经过原点.若存在,写出直线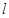 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
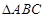 的顶点
的顶点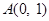 ,
,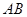 边上的中线
边上的中线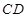 所在的直线方程为
所在的直线方程为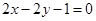 ,
,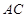 边上的高
边上的高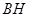 所在直线的方程为
所在直线的方程为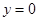 。
。(1)求
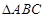 的顶点
的顶点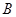 、
、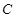 的坐标;
的坐标;(2)若圆
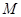 经过不同的三点
经过不同的三点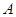 、
、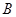 、
、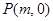 ,且斜率为
,且斜率为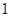 的直线与圆
的直线与圆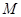 相切于点
相切于点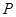 ,求圆
,求圆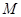 的方程;
的方程;(3)问圆
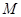 是否存在斜率为
是否存在斜率为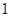 的直线
的直线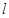 ,使
,使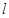 被圆
被圆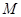 截得的弦为
截得的弦为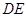 ,以
,以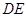 为直径的圆经过原点.若存在,写出直线
为直径的圆经过原点.若存在,写出直线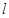 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。(1) 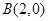 ,
, 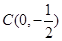 ;(2)
;(2) 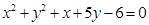 ;
;
(3)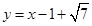 或
或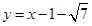 。
。
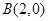 ,
, 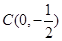 ;(2)
;(2) 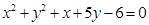 ;
;(3)
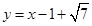 或
或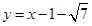 。
。试题分析:(1)
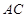 边上的高
边上的高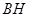 所在直线的方程为
所在直线的方程为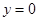 ,所以,
,所以,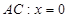 ,
,又
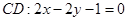 ,所以
,所以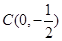 2分
2分设
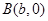 ,则
,则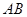 的中点
的中点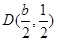 ,代入方程
,代入方程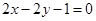 ,
,解得
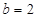 ,所以
,所以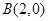 . 4分
. 4分(2)由
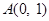 ,
,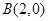 可得,圆
可得,圆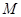 的弦
的弦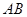 的中垂线方程为
的中垂线方程为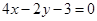 ,
,注意到
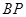 也是圆
也是圆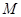 的弦,所以,圆心在直线
的弦,所以,圆心在直线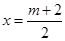 上,
上,设圆心
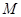 坐标为
坐标为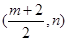 ,
,因为圆心
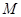 在直线
在直线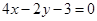 上,所以
上,所以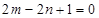 ①,
①,又因为斜率为
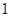 的直线与圆
的直线与圆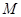 相切于点
相切于点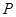 ,所以
,所以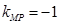 ,
,即
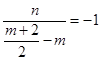 ,整理得
,整理得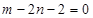 ②,
②, 由①②解得
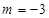 ,
,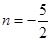 ,
,所以,
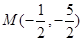 ,半径
,半径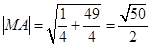 ,
,所以所求圆方程为
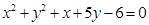 。 8分
。 8分(3)假设存在直线
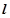 ,不妨设所求直线
,不妨设所求直线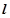 方程为
方程为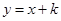 ,
,
联立方程
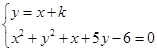 得:
得: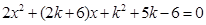 9分
9分又
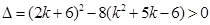 得
得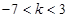 10分
10分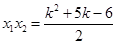 ,
, 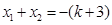 ,
,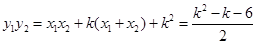 11分
11分依题意得
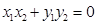 12分
12分故
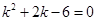 解得:
解得: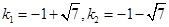 13分
13分经验证,满足题意。故所求直线方程为:
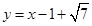 或
或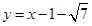 14分
14分点评:此题主要考查了直线与圆的位置关系,涉及的知识较多,综合性较强。知识点的灵活应用是解题的关键,是一道中档题。

练习册系列答案
相关题目
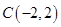 ,过点C作两条互相垂直的直线
,过点C作两条互相垂直的直线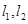 ,
,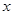 轴、
轴、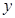 轴交于点A、
轴交于点A、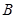 ,设点
,设点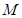 是线段
是线段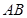 的中点,则点M的轨迹方程为( )
的中点,则点M的轨迹方程为( )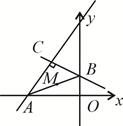
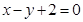 B.
B.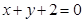
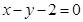 D.
D.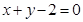
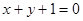 被圆
被圆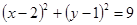 所截得的弦长为 ;
所截得的弦长为 ;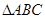 三个顶点的坐标为A(a,0),B(0,b),C(0,c),点D(d,0)在线段OA上(异于端点),设a,b,c,d均为非零实数,直线BD交AC于点E,则OE所在的直线方程为 _
三个顶点的坐标为A(a,0),B(0,b),C(0,c),点D(d,0)在线段OA上(异于端点),设a,b,c,d均为非零实数,直线BD交AC于点E,则OE所在的直线方程为 _  与
与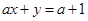 平行,则
平行,则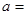
 平行,则k的值是
平行,则k的值是
 与直线
与直线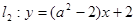 平行,则
平行,则 的值为 ( )
的值为 ( )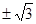
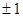
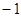
 过点A(1,2),B(2,3),则直线
过点A(1,2),B(2,3),则直线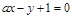 上,则直线l1与直线l2:
上,则直线l1与直线l2: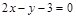 的位置关系是 .(填“平行”或“垂直”)
的位置关系是 .(填“平行”或“垂直”)