题目内容
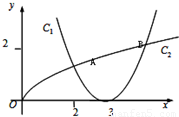
函数f(x)=(x-3)2和g(x)= 的图象的示意图如图所示,设两函数的图象交于点A(x1,y1)B(x2,y2),且x1<x2.
的图象的示意图如图所示,设两函数的图象交于点A(x1,y1)B(x2,y2),且x1<x2. (1)请指出示意图中曲线C1,C2分别对应哪一个函数?
(2)若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{0,1,2,3,4,5,6}指出a,b的值,并说明理由.
【答案】分析:(1)结合所给的函数解析式以及所给的函数图象,直接可得示意图中曲线C1,C2分别对应的函数解析式.
(2)令h(x)=f(x)-g(x),分别求得x=0、1、2、3、4、5、6时的函数值,再利用函数零点的判定定理求得a,b的值.
解答:解:(1)曲线C1对应函数为f(x)=(x-3)2 ,C2对应函数为g(x)=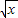 .…4分
.…4分
(2)令h(x)=f(x)-g(x)=(x-3)2 - ,分别令 x=0、1、2、3、4、5、6计算可得
,分别令 x=0、1、2、3、4、5、6计算可得
h(1)=3>0,h(2)=1-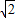 <0,
<0,
从而h(x)在区间[1,2]有一个零点,所以x1∈[1,2],即a=1.…9分
h(4)=-1<0,h(5)=4-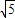 >0,同理可知 x2∈[4,5],即b=4.…14分
>0,同理可知 x2∈[4,5],即b=4.…14分
点评:本题主要考查函数的图象和性质,以及数形结合能力,函数零点的判定定理的应用,属于基础题.
(2)令h(x)=f(x)-g(x),分别求得x=0、1、2、3、4、5、6时的函数值,再利用函数零点的判定定理求得a,b的值.
解答:解:(1)曲线C1对应函数为f(x)=(x-3)2 ,C2对应函数为g(x)=
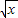 .…4分
.…4分(2)令h(x)=f(x)-g(x)=(x-3)2 -
 ,分别令 x=0、1、2、3、4、5、6计算可得
,分别令 x=0、1、2、3、4、5、6计算可得h(1)=3>0,h(2)=1-
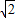 <0,
<0,从而h(x)在区间[1,2]有一个零点,所以x1∈[1,2],即a=1.…9分
h(4)=-1<0,h(5)=4-
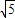 >0,同理可知 x2∈[4,5],即b=4.…14分
>0,同理可知 x2∈[4,5],即b=4.…14分点评:本题主要考查函数的图象和性质,以及数形结合能力,函数零点的判定定理的应用,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目